10. Canonical permutation
Finally, we give an algorithm that canonicalize simultaneously the free and the dummy/repeated indices. The algorithm always canonicalizes first the free indices and then the dummy/repeated indices.
Portugal's example in paper II. Suppose a tensor with 12 indices whose index-configuration is described by the following permutation:
In[297]:=
![]()
In[298]:=
![]()
Out[298]=
![]()
The symmetries of the tensor are described by this GS:
In[299]:=
![]()
1) Canonical configuration assuming that all indices are free (empty DummySet/RepeatedSet expressions):
In[300]:=
![]()
![]()
![]()
Out[300]=
![]()
In[301]:=
![]()
Out[301]=
![]()
In[302]:=
![]()
Out[302]=
![]()
Let us check that this is the smallest permutation in the right coset S.g. We work in Images notation because only then the sorting process is apparent:
In[303]:=
![]()
Out[303]=
![]()
In[304]:=
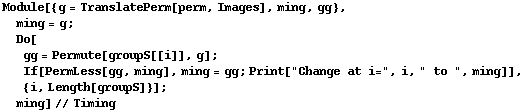
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Out[304]=
![]()
2) Now suppose that indices 1,2 (in the canonical list) are free while the others are contracted as given by the list of pairs or slots {{3,4},{5,6},{7,8},{9,10},{11,12}}. The canonical configuration is (note that this is the result quoted by Portugal et al.):
In[305]:=
![]()
![]()
![]()
![]()
Out[305]=
![]()
In[306]:=
![]()
Out[306]=
![]()
In[307]:=
![]()
Out[307]=
![]()
Note that this permutation is smaller than the one obtained using only the right coset S.g. This is obvious because the double coset S.g.D contains the right coset S.g. Again, we check that this is the right answer by brute force. We construct the SGS of the group D and search for the least of the permutations of the double coset S.g.D. Do not evaluate the Module below because it takes very long (the cell has been made nonevaluatable):
In[308]:=
![]()
Out[308]=
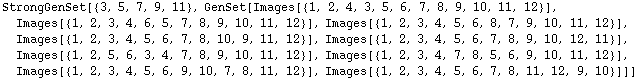
In[309]:=
![]()
Out[309]=
![]()
In[310]:=
3) With OrderedBase→False we can get a different result, because we are sorting indices with a different base:
In[311]:=
![]()
![]()
![]()
![]()
Out[311]=
![]()
In[312]:=
![]()
Out[312]=
![]()
In[313]:=
![]()
Out[313]=
![]()
That result can also be interpreted in terms of an ordering of permutations with respect to a particular base. In this case the dummy indices are sorted differently (again, this cell has been made nonevaluatable):
In[314]:=
CanonicalPerm Compute a canonical representative given the free and dummy indices of an object
TimeVerbose Timings information
xPermVerbose Detailed information of the internal processes
OrderedBase Fill missing points in base with sorted points
Index canonicalization
| Created by Mathematica (May 16, 2008) |