3.2. Cosets and double cosets
All cosets of a given subgroup of permutations have the same order, and partition the full group. Hence the order of a subgroup divides the order of the full group (Lagrange theorem).
Suppose we start with the full group S5 of permutations:
In[75]:=
![]()
Out[75]=
![]()
One of its subgroups is S3:
In[76]:=
![]()
Out[76]=
![]()
There are therefore 20 left-cosets of S4 in S5, that we call L1...L20:
In[77]:=
![]()
Out[77]=
| {Images[{1,2,3,4,5}],Images[{1,3,2,4,5}],Images[{2,1,3,4,5}],Images[{2,3,1,4,5}],Images[{3,1,2,4,5}],Images[{3,2,1,4,5}]} |
| {Images[{1,2,3,5,4}],Images[{1,3,2,5,4}],Images[{2,1,3,5,4}],Images[{2,3,1,5,4}],Images[{3,1,2,5,4}],Images[{3,2,1,5,4}]} |
| {Images[{1,2,4,3,5}],Images[{1,3,4,2,5}],Images[{2,1,4,3,5}],Images[{2,3,4,1,5}],Images[{3,1,4,2,5}],Images[{3,2,4,1,5}]} |
| {Images[{1,2,4,5,3}],Images[{1,3,4,5,2}],Images[{2,1,4,5,3}],Images[{2,3,4,5,1}],Images[{3,1,4,5,2}],Images[{3,2,4,5,1}]} |
| {Images[{1,2,5,3,4}],Images[{1,3,5,2,4}],Images[{2,1,5,3,4}],Images[{2,3,5,1,4}],Images[{3,1,5,2,4}],Images[{3,2,5,1,4}]} |
| {Images[{1,2,5,4,3}],Images[{1,3,5,4,2}],Images[{2,1,5,4,3}],Images[{2,3,5,4,1}],Images[{3,1,5,4,2}],Images[{3,2,5,4,1}]} |
| {Images[{1,4,2,3,5}],Images[{1,4,3,2,5}],Images[{2,4,1,3,5}],Images[{2,4,3,1,5}],Images[{3,4,1,2,5}],Images[{3,4,2,1,5}]} |
| {Images[{1,4,2,5,3}],Images[{1,4,3,5,2}],Images[{2,4,1,5,3}],Images[{2,4,3,5,1}],Images[{3,4,1,5,2}],Images[{3,4,2,5,1}]} |
| {Images[{1,4,5,2,3}],Images[{1,4,5,3,2}],Images[{2,4,5,1,3}],Images[{2,4,5,3,1}],Images[{3,4,5,1,2}],Images[{3,4,5,2,1}]} |
| {Images[{1,5,2,3,4}],Images[{1,5,3,2,4}],Images[{2,5,1,3,4}],Images[{2,5,3,1,4}],Images[{3,5,1,2,4}],Images[{3,5,2,1,4}]} |
| {Images[{1,5,2,4,3}],Images[{1,5,3,4,2}],Images[{2,5,1,4,3}],Images[{2,5,3,4,1}],Images[{3,5,1,4,2}],Images[{3,5,2,4,1}]} |
| {Images[{1,5,4,2,3}],Images[{1,5,4,3,2}],Images[{2,5,4,1,3}],Images[{2,5,4,3,1}],Images[{3,5,4,1,2}],Images[{3,5,4,2,1}]} |
| {Images[{4,1,2,3,5}],Images[{4,1,3,2,5}],Images[{4,2,1,3,5}],Images[{4,2,3,1,5}],Images[{4,3,1,2,5}],Images[{4,3,2,1,5}]} |
| {Images[{4,1,2,5,3}],Images[{4,1,3,5,2}],Images[{4,2,1,5,3}],Images[{4,2,3,5,1}],Images[{4,3,1,5,2}],Images[{4,3,2,5,1}]} |
| {Images[{4,1,5,2,3}],Images[{4,1,5,3,2}],Images[{4,2,5,1,3}],Images[{4,2,5,3,1}],Images[{4,3,5,1,2}],Images[{4,3,5,2,1}]} |
| {Images[{4,5,1,2,3}],Images[{4,5,1,3,2}],Images[{4,5,2,1,3}],Images[{4,5,2,3,1}],Images[{4,5,3,1,2}],Images[{4,5,3,2,1}]} |
| {Images[{5,1,2,3,4}],Images[{5,1,3,2,4}],Images[{5,2,1,3,4}],Images[{5,2,3,1,4}],Images[{5,3,1,2,4}],Images[{5,3,2,1,4}]} |
| {Images[{5,1,2,4,3}],Images[{5,1,3,4,2}],Images[{5,2,1,4,3}],Images[{5,2,3,4,1}],Images[{5,3,1,4,2}],Images[{5,3,2,4,1}]} |
| {Images[{5,1,4,2,3}],Images[{5,1,4,3,2}],Images[{5,2,4,1,3}],Images[{5,2,4,3,1}],Images[{5,3,4,1,2}],Images[{5,3,4,2,1}]} |
| {Images[{5,4,1,2,3}],Images[{5,4,1,3,2}],Images[{5,4,2,1,3}],Images[{5,4,2,3,1}],Images[{5,4,3,1,2}],Images[{5,4,3,2,1}]} |
In[78]:=
![]()
And they all form the full S5 group:
In[79]:=
![]()
Out[79]=
![]()
The concept of double coset will be important for us later. A double coset of two subgroups H and K in the full group G is the set of permutations of the form h.g.k for all h in H, all k in K and a particular g in G. The double cosets also partition the full group G, but unfortunately they do not all have the same size, and therefore there is not an equivalent of the Lagrange theorem for double cosets. The computation of the number of double cosets in a group G is a nontrivial task.
Construct another subgroup of S5:
In[80]:=
![]()
Out[80]=
![]()
That means that there are 15 right-cosets of H in S5, that we call R1...R15:
In[81]:=
![]()
Out[81]=
| {Images[{1,2,3,4,5}],Images[{1,2,4,3,5}],Images[{2,1,3,4,5}],Images[{2,1,4,3,5}],Images[{3,4,1,2,5}],Images[{3,4,2,1,5}],Images[{4,3,1,2,5}],Images[{4,3,2,1,5}]} |
| {Images[{1,2,3,5,4}],Images[{1,2,5,3,4}],Images[{2,1,3,5,4}],Images[{2,1,5,3,4}],Images[{3,5,1,2,4}],Images[{3,5,2,1,4}],Images[{5,3,1,2,4}],Images[{5,3,2,1,4}]} |
| {Images[{1,2,4,5,3}],Images[{1,2,5,4,3}],Images[{2,1,4,5,3}],Images[{2,1,5,4,3}],Images[{4,5,1,2,3}],Images[{4,5,2,1,3}],Images[{5,4,1,2,3}],Images[{5,4,2,1,3}]} |
| {Images[{1,3,2,4,5}],Images[{1,3,4,2,5}],Images[{2,4,1,3,5}],Images[{2,4,3,1,5}],Images[{3,1,2,4,5}],Images[{3,1,4,2,5}],Images[{4,2,1,3,5}],Images[{4,2,3,1,5}]} |
| {Images[{1,3,2,5,4}],Images[{1,3,5,2,4}],Images[{2,5,1,3,4}],Images[{2,5,3,1,4}],Images[{3,1,2,5,4}],Images[{3,1,5,2,4}],Images[{5,2,1,3,4}],Images[{5,2,3,1,4}]} |
| {Images[{1,3,4,5,2}],Images[{1,3,5,4,2}],Images[{3,1,4,5,2}],Images[{3,1,5,4,2}],Images[{4,5,1,3,2}],Images[{4,5,3,1,2}],Images[{5,4,1,3,2}],Images[{5,4,3,1,2}]} |
| {Images[{1,4,2,3,5}],Images[{1,4,3,2,5}],Images[{2,3,1,4,5}],Images[{2,3,4,1,5}],Images[{3,2,1,4,5}],Images[{3,2,4,1,5}],Images[{4,1,2,3,5}],Images[{4,1,3,2,5}]} |
| {Images[{1,4,2,5,3}],Images[{1,4,5,2,3}],Images[{2,5,1,4,3}],Images[{2,5,4,1,3}],Images[{4,1,2,5,3}],Images[{4,1,5,2,3}],Images[{5,2,1,4,3}],Images[{5,2,4,1,3}]} |
| {Images[{1,4,3,5,2}],Images[{1,4,5,3,2}],Images[{3,5,1,4,2}],Images[{3,5,4,1,2}],Images[{4,1,3,5,2}],Images[{4,1,5,3,2}],Images[{5,3,1,4,2}],Images[{5,3,4,1,2}]} |
| {Images[{1,5,2,3,4}],Images[{1,5,3,2,4}],Images[{2,3,1,5,4}],Images[{2,3,5,1,4}],Images[{3,2,1,5,4}],Images[{3,2,5,1,4}],Images[{5,1,2,3,4}],Images[{5,1,3,2,4}]} |
| {Images[{1,5,2,4,3}],Images[{1,5,4,2,3}],Images[{2,4,1,5,3}],Images[{2,4,5,1,3}],Images[{4,2,1,5,3}],Images[{4,2,5,1,3}],Images[{5,1,2,4,3}],Images[{5,1,4,2,3}]} |
| {Images[{1,5,3,4,2}],Images[{1,5,4,3,2}],Images[{3,4,1,5,2}],Images[{3,4,5,1,2}],Images[{4,3,1,5,2}],Images[{4,3,5,1,2}],Images[{5,1,3,4,2}],Images[{5,1,4,3,2}]} |
| {Images[{2,3,4,5,1}],Images[{2,3,5,4,1}],Images[{3,2,4,5,1}],Images[{3,2,5,4,1}],Images[{4,5,2,3,1}],Images[{4,5,3,2,1}],Images[{5,4,2,3,1}],Images[{5,4,3,2,1}]} |
| {Images[{2,4,3,5,1}],Images[{2,4,5,3,1}],Images[{3,5,2,4,1}],Images[{3,5,4,2,1}],Images[{4,2,3,5,1}],Images[{4,2,5,3,1}],Images[{5,3,2,4,1}],Images[{5,3,4,2,1}]} |
| {Images[{2,5,3,4,1}],Images[{2,5,4,3,1}],Images[{3,4,2,5,1}],Images[{3,4,5,2,1}],Images[{4,3,2,5,1}],Images[{4,3,5,2,1}],Images[{5,2,3,4,1}],Images[{5,2,4,3,1}]} |
In[82]:=
![]()
Now we want to find the number of double cosets of H and S3 in S5. The key idea is that a permutation in H acting on a left coset Li gives another (perhaps the same) left coset Lj. Therefore permutations in H now act as permutations on a set in which the points are the left cosets L1...L20. Each orbit in this set corresponds to a double coset. Note that double cosets are disjoint unions of single-cosets of each of the two subgroups.
We first have the product group, with 24 elements (it is actually S4):
In[83]:=
![]()
Out[83]=
![]()
This double coset contains the following single cosets:
In[84]:=
![]()
Out[84]=
![]()
In[85]:=
![]()
Out[85]=
![]()
Now we look for the double coset containing L2. It is again S4 with points 4 and 5 exchanged:
In[86]:=
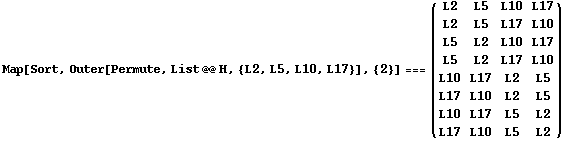
Out[86]=
![]()
In[87]:=
![]()
Out[87]=
![]()
In[88]:=
![]()
Out[88]=
![]()
Now we look for the double coset containing L4:
In[89]:=
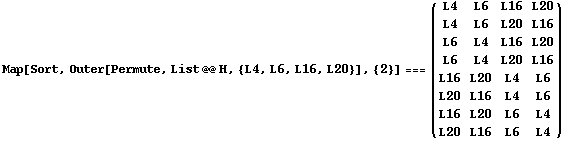
Out[89]=
![]()
In[90]:=
![]()
Out[90]=
![]()
In[91]:=
![]()
Out[91]=
![]()
Now we look for the double coset containing L8:
In[92]:=
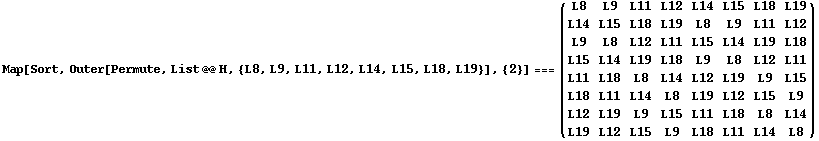
Out[92]=
![]()
In[93]:=
![]()
Out[93]=
![]()
In[94]:=
![]()
Out[94]=
![]()
We conclude that there are 4 double cosets, three of them with order 24 and the last one with order 48. They all form the full group S5:
In[95]:=
![]()
Out[95]=
![]()
Tidy up:
In[96]:=
![]()
There are also commands to form transversals.
LeftTransversal Transversal of left cosets
RightTransversal Transversal of right cosets
DoubleTransversal Transversal of double cosets
Transversals.
| Created by Mathematica (May 16, 2008) |