0.1. Example session
This is a very simple example of the use of xTensor`. We start by defining a manifold and some tensor fields living on its tangent bundle.
Define a 3d manifold M3:
In[10]:=
![]()
![]()
![]()
Define a contravariant vector v and a covariant antisymmetric tensor F:
In[11]:=
![]()
![]()
![]()
![]()
Tensor product of both tensors, based on the abstract index notation:
In[13]:=
![]()
Out[13]=
![]()
In[14]:=
![]()
Out[14]=
![]()
There is no automatic simplification. It must be explicitly asked for:
In[15]:=
![]()
Out[15]=
![]()
Example of dummy handling:
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
![]()
There is not a metric and hence v cannot be covariant. Note the position of the head ERROR:
In[18]:=
![]()
![]()
![]()
Out[18]=
![]()
Internal structure:
In[19]:=
![]()
Out[19]//InputForm=
(F[-a, -c] - 3*F[-a, -d]*F[-c, d])*v[-b]*v[b]*v[c]
Now we define a covariant derivative operator and check the first Bianchi identity (valid for any symmetric connection). Note that xTensor` uses unique (dollar-) variables as internal dummy indices to avoid index collisions. The function ScreenDollarIndices hides those indices replacing them by "normal" indices.
Covariant derivatives are defined by default with curvature but without torsion:
In[20]:=
![]()
Out[20]=

In[21]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[22]:=
![]()
Out[22]=
![]()
In[23]:=
![]()
Out[23]=
![]()
The tensors have been defined with their expected symmetries:
In[24]:=
![]()
Out[24]=
![]()
but it is possible to deduce them from more basic principles:
In[25]:=
![]()
Out[25]=
![]()
In[26]:=
![]()
Out[26]=
![]()
Check of the second Bianchi identity:
In[27]:=
![]()
Out[27]=
![]()
In[28]:=
![]()
Out[28]=
![]()
In[29]:=
![]()
Out[29]=
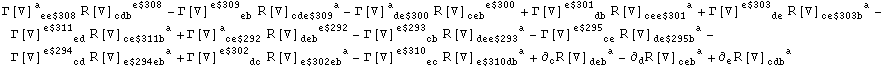
In[30]:=
![]()
Out[30]=
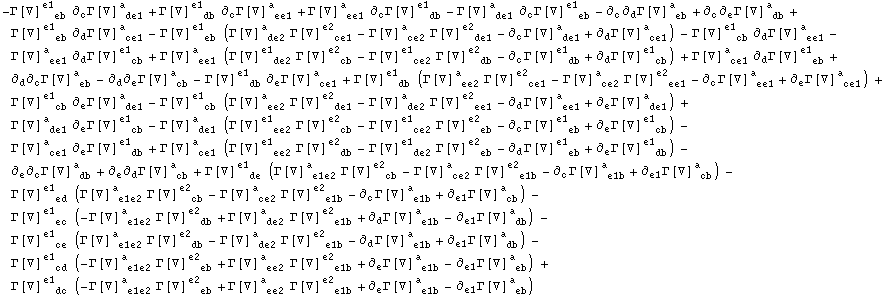
In[31]:=
![]()
Out[31]=
![]()
Commutation of covariant derivatives. It is possible to choose the indices (use CommuteCovDs) or just let xTensor` to bring the derivative indices into canonical order (use SortCovDs):
In[32]:=
![]()
Out[32]=
![]()
In[33]:=
![]()
Out[33]=
![]()
In[34]:=
![]()
Out[34]=
![]()
Now we introduce a metric on the manifold. Its associated curvature tensors are defined: RiemannCD, RiciCD, EinsteinCD, etc:
In[35]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[36]:=
![]()
Out[36]=
![]()
In[37]:=
![]()
Out[37]=
![]()
In[38]:=
![]()
Out[38]=
![]()
In[39]:=
![]()
Out[39]=
![]()
Let us check the antisymmetry of the second pair of indices in the Riemann tensor:
In[40]:=
![]()
Out[40]=
![]()
Because canonicalization is not automatic, the previous expression is not automatically zero. We expand it in derivatives of Christoffels and canonicalize. The partial derivative does not commute with the metric, so that internally the code replaces temporarily those derivatives with Levi-Civita connections:
In[41]:=
![]()
![]()
![]()
![]()
![]()
Out[41]=
![]()
Metric contraction is not automatic either. The resulting expression is not obviously zero:
In[42]:=
![]()
Out[42]=
![]()
Actually it is only zero for connections deriving from a metric:
In[43]:=
![]()
Out[43]=
![]()
In[44]:=
![]()
Out[44]=
![]()
In this case a simple reordering of the partial derivatives (this is not automatic) would have been enough:
In[45]:=
![]()
Out[45]=
![]()
Examples of Lie derivative and bracket:
In[46]:=
![]()
Out[46]=
![]()
In[47]:=
![]()
Out[47]=
![]()
Undefine all objects on the manifold and the manifold itself:
In[48]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[49]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[51]:=
![]()
![]()
![]()
There are no symbols left in the Global` context
In[52]:=
![]()
![]()
| Created by Mathematica (May 16, 2008) |