6.3. General Bianchi identities

Let us now check the Bianchi identities for general covariant derivatives with torsion. Note that these identities are not directly encoded in xTensor`, but can be easily computed.

Define a covariant derivative with torsion. Note the special symmetry properties of the defined tensors:

In[462]:=

This is the general form of the first Bianchi identity:

In[463]:=

Out[463]=

In[464]:=

Out[464]=

The computation can be performed by transforming the derivative CD and its associated tensors into PD and Christoffel tensors:

In[465]:=

Out[465]=

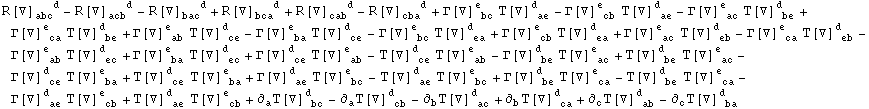
In[466]:=

Out[466]=

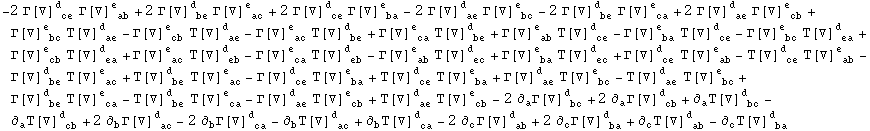
In[467]:=

Out[467]=

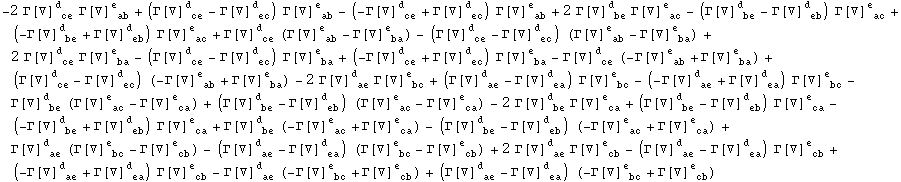
In[468]:=

Out[468]=

This is the general form of the second Bianchi identity:

In[469]:=

Out[469]=

In[470]:=

Out[470]=

The computation proceeds along the same lines:

In[471]:=

Out[471]=

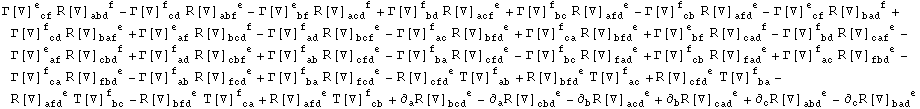
In[472]:=

Out[472]=

In[473]:=

Out[473]=

In[474]:=

Out[474]=

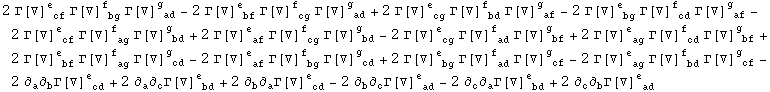
In[475]:=

Out[475]=

Clean up:

In[476]:=

Created by Mathematica  (May 16, 2008)