7.8. Induced metrics

xTensor` has a simple way to define the induced metric obtained from projection of another metric along hypersurface-orthogonal vector fields, as it is typically done in the ADM 3+1 decomposition of the spacetime metric:

We first define the global ambient metric:

In[632]:=

DefMetric[-1, metricg[-a, -b], CD, {";", "▽"}, PrintAs->"g"] ;

** DefTensor: Defining symmetric metric tensor metricg[-a, -b] .

** DefTensor: Defining antisymmetric tensor epsilonmetricg[a, b, c] .

** DefCovD: Defining covariant derivative CD[-a] .

** DefTensor: Defining vanishing torsion tensor TorsionCD[a, -b, -c] .

** DefTensor: Defining symmetric Christoffel tensor ChristoffelCD[a, -b, -c] .

** DefTensor: Defining Riemann tensor RiemannCD[-a, -b, -c, -d] .

** DefTensor: Defining symmetric Ricci tensor RicciCD[-a, -b] .

** DefCovD:  Contractions of Riemann automatically replaced by Ricci.

** DefTensor: Defining Ricci scalar RicciScalarCD[] .

** DefCovD:  Contractions of Ricci automatically replaced by RicciScalar.

** DefTensor: Defining symmetric Einstein tensor EinsteinCD[-a, -b] .

** DefTensor: Defining vanishing Weyl tensor WeylCD[-a, -b, -c, -d] .

** DefTensor: Defining symmetric TFRicci tensor TFRicciCD[-a, -b] .

   Rules {1, 2} have been declared as DownValues for TFRicciCD .

** DefCovD:  Computing RiemannToWeylRules for dim 3

** DefCovD:  Computing RicciToTFRicci for dim 3

** DefCovD:  Computing RicciToEinsteinRules for dim 3

Define the timelike normal to the slices. The use of MakeRule and AutomaticRules will be explained later.

In[633]:=

DefTensor[n[a], M3]

** DefTensor: Defining tensor n[a] .

In[634]:=

AutomaticRules[n, MakeRule[{n[a] n[-a], -1}]]

   Rules {1} have been declared as UpValues for n .

In[635]:=

AutomaticRules[n, MakeRule[{metricg[-a, -b] n[a] n[b], -1}]]

   Rules {1, 2} have been declared as UpValues for n .

We choose the conventions as in Choptuik:

In[636]:=

$ExtrinsicKSign = -1 ;

$AccelerationSign = -1 ;

Now we can define the induced metric associated to the pair {ambient metric, orthogonal vector field}. Note that even though there is another metric on the tangent bundle, an induced metric is not considered to be a frozen metric.

In[638]:=

DefMetric[1, metrich[-a, -b], cd, {"|", "D"}, InducedFrom→ {metricg, n}, PrintAs->"h"]

DefMetric :: old : There are already metrics {metricg} in vbundle TangentM3. Defined metric is frozen.

** DefTensor: Defining symmetric metric tensor metrich[-a, -b] .

** DefTensor: Defining antisymmetric tensor epsilonmetrich[a, b] .

** DefCovD: Defining covariant derivative cd[-a] .

** DefTensor: Defining vanishing torsion tensor Torsioncd[a, -b, -c] .

** DefTensor: Defining symmetric Christoffel tensor Christoffelcd[a, -b, -c] .

** DefTensor: Defining Riemann tensor Riemanncd[-a, -b, -c, -d] .

** DefTensor: Defining symmetric Ricci tensor Riccicd[-a, -b] .

** DefCovD:  Contractions of Riemann automatically replaced by Ricci.

** DefTensor: Defining Ricci scalar RicciScalarcd[] .

** DefCovD:  Contractions of Ricci automatically replaced by RicciScalar.

** DefTensor: Defining symmetric Einstein tensor Einsteincd[-a, -b] .

** DefTensor: Defining vanishing Weyl tensor Weylcd[-a, -b, -c, -d] .

** DefTensor: Defining symmetric TFRicci tensor TFRiccicd[-a, -b] .

   Rules {1, 2} have been declared as DownValues for TFRiccicd .

** DefCovD:  Computing RiemannToWeylRules for dim 3

** DefCovD:  Computing RicciToTFRicci for dim 3

** DefCovD:  Computing RicciToEinsteinRules for dim 3

** DefTensor: Defining extrinsic curvature tensor ExtrinsicKmetrich[a, b] . Associated to vector n

** DefTensor: Defining acceleration vector Accelerationn[a] . Associated to vector n

** DefInertHead: Defining projector inert-head Projectormetrich.

For a hypersurface orthogonal vector we can express the acceleration vector in terms of a lapse function:

In[639]:=

DefTensor[lapse[], M3, PrintAs->"α"]

** DefTensor: Defining tensor lapse[] .

In[640]:=

LapseRule = Accelerationn[a_] →cd[a][lapse[]]/lapse[]

Out[640]=

An_ ^Underscript[a, _] → (D_ ^aα_^)/α_^

We define a generic vector field and a spatial vector field:

In[641]:=

DefTensor[V[-a], M3]

** DefTensor: Defining tensor V[-a] .

In[642]:=

DefTensor[W[-a], M3, OrthogonalTo→ {n[a]}, ProjectedWith→ {metrich[a, -b]}]

** DefTensor: Defining tensor W[-a] .

The first operation we need is the decomposition of any expression along the normal vector. This is given by the command InducedDecomposition, which requires as second argument the pair {projector, normal}. The decomposition process does not change the input; it simply rewrites it in a different way:

Any expression can be decomposed in projected and orthogonal parts with respect to the vector field. Note the special output of the head Projectormetrich:

In[643]:=

InducedDecomposition[W[-a], {metrich, n}]

Out[643]=

W_a^

In[644]:=

InducedDecomposition[V[-a], {metrich, n}]

Out[644]=

Underscript[P, h][V_a^ ] - n_a^ Scalar[n_ ^a V_a^ ]

In[645]:=

InducedDecomposition[7V[-a] V[-b] + W[-a] W[-b], {metrich, n}]

Out[645]=

7 (Underscript[P, h][V_a^ ] - n_a^ Scalar[n_ ^a V_a^ ]) (Underscript[P, h][V_b^ ] - n_b^ Scalar[n_ ^a V_a^ ]) + W_a^ W_b^

In[646]:=

InducedDecomposition[RiemannCD[-a, -b, -c, -d], {metrich, n}]

Out[646]=

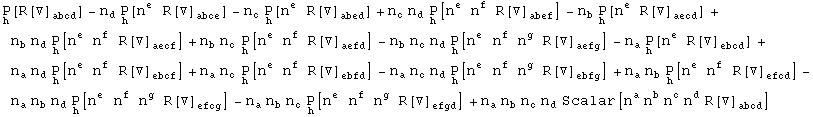
In[647]:=

ToCanonical[%]

Out[647]=

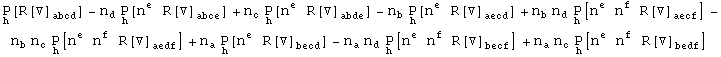
Projection along the normal vector is automatic:

In[648]:=

n[d] %//Expand

Out[648]=

In[649]:=

n[c] %//Expand

Out[649]=

0

In[650]:=

n[b] %%//Expand

Out[650]=

Underscript[P, h][n_ ^b n_ ^d R[▽] _abcd^    ]

The head Projectormetrich is the formal projector, but we now need a command which actually performs the projection. This is done with ProjectWith[metrich]. Do not confuse them. They have been constructed as a matched pair, and it is very useful to go from the former to the latter.

As long as we need to work only with the projected part of RicciCD, we can use this object:

In[651]:=

Projectormetrich[RicciCD[-a, -b]]

Out[651]=

Underscript[P, h][R[▽] _ab^  ]

However, if we need to perform the projection, we can do this:

In[652]:=

%/.Projectormetrich→ProjectWith[metrich]

Out[652]=

h_a ^( c) h_b ^( d) R[▽] _cd^  

Finally, we can expand the projectors as

In[653]:=

%//ProjectorToMetric

Out[653]=

(δ_a ^( c) + n_a^ n_ ^c) (δ_b ^( d) + n_b^ n_ ^d) R[▽] _cd^  

In[654]:=

%//Expand

Out[654]=

R[▽] _ab^   + n_b^ n_ ^c R[▽] _ac^   + n_a^ n_ ^c R[▽] _cb^   + n_a^ n_b^ n_ ^c n_ ^d R[▽] _cd^  

The projection process can be easily undone using InducedDecomposition:

In[655]:=

InducedDecomposition[%, {metrich, n}]//ToCanonical

Out[655]=

Underscript[P, h][R[▽] _ab^  ]

InducedDecomposition    Decompose an expression along the normal vector
Projector                Formal projector head
ProjectWith                Actual projection operator, using the projected metric
ProjectorToMetric        Convert projected metric into sum of metric and projector onto the normal
MetricToProjector        Convert metric into sum of projected metric and projector onto the normal

Projection operators.

The second issue is the manipulation of derivatives. The projected metric has its own Levi-Civita connection, which is a proper covariant derivative only when acting on objects on the projected manifold. The relation between the original and the new covariant derivatives is given by  a kind of "Christoffel" encoded in two objects: the extrinsic curvature ExtrinsicK tensor and the Acceleration vector:

This is the derivative of the normal (note the sign convention):

In[656]:=

CD[-a][n[b]]

Out[656]=

▽_a^ n_ ^b

In[657]:=

%//GradNormalToExtrinsicK

Out[657]=

-Kh_a ^( b) - An_ ^b n_a^

It is useful to remove derivatives in favour of these two tensors whenever possible. For example for "spatial" vectors:

In[658]:=

n[-a] CD[-b][W[a]]

Out[658]=

n_a^ (▽_b^ W_ ^a)

In[659]:=

%//GradNormalToExtrinsicK//ContractMetric

Out[659]=

Kh_b ^( a) W_a^ + An_ ^a n_b^ W_a^

The opposite command also exists:

In[660]:=

ExtrinsicKmetrich[-a, -b]

Out[660]=

Kh_ab^  

In[661]:=

%//ExtrinsicKToGradNormal//ContractMetric

Out[661]=

-An_b^ n_a^ - ▽_a^ n_b^

Let us now project the derivative on a "spatial" vector:

In[662]:=

CD[-c][W[-b]]

Out[662]=

▽_c^ W_b^

In[663]:=

%//ProjectWith[metrich]

Out[663]=

h_b ^( a) h_c ^( d) (▽_d^ W_a^ )

In[664]:=

%//ProjectorToMetric

Out[664]=

(δ_b ^( a) + n_ ^a n_b^ ) (δ_c ^( d) + n_c^ n_ ^d) (▽_d^ W_a^ )

In[665]:=

%//Expand

Out[665]=

n_ ^a n_c^ (▽_a^ W_b^ ) + n_ ^a n_b^ (▽_c^ W_a^ ) + ▽_c^ W_b^ + n_ ^a n_b^ n_c^ n_ ^d (▽_d^ W_a^ )

In[666]:=

%//GradNormalToExtrinsicK

Out[666]=

-n_b^ (-Kh_c ^( a) - An_ ^a n_c^ ) W_a^ - n_b^ n_c^ (-Kh_d ^( a) - An_ ^a n_d^ ) n_ ^d W_a^ + n_ ^a n_c^ (▽_a^ W_b^ ) + ▽_c^ W_b^

In[667]:=

%//Simplification

Out[667]=

Kh_ca^   n_b^ W_ ^a + n_ ^a n_c^ (▽_a^ W_b^ ) + ▽_c^ W_b^

A different way to do it is this:

In[668]:=

cd[-c][W[-b]]

Out[668]=

D_c^ W_b^

In[669]:=

ProjectDerivative[%]

Out[669]=

Underscript[P, h][▽_c^ W_b^ ]

In[670]:=

%/.Projectormetrich→ProjectWith[metrich]

Out[670]=

h_b ^( a) h_c ^( d) (▽_d^ W_a^ )

ExtrinsicK                Extrinsic curvature tensor
Acceleration            Acceleration vector
GradNormalToExtrinsicK    Convert from derivatives of the normal to the extrinsic curvature tensor
ExtrinsicKToGradNormal    Convert form the extrinsic curvature tensor to derivatives of the normal
ProjectDerivative        Convert derivatives on the projected vbundle into projected derivatives

Induced derivatives.

A very important detail is that of the Leibnitz rule for induced derivatives. It is not valid on expressions not on the projected vbundle!

The vector W lives on the projected vbundle and therefore the Leibnitz rule is valid:

In[671]:=

cd[-a][W[b] W[c]]

Out[671]=

W_ ^c (D_a^ W_ ^b) + W_ ^b (D_a^ W_ ^c)

If there are free non-spatial indices we throw an error message:

In[672]:=

Catch @ cd[-a][V[b] V[c]]

Validate :: error : Induced derivative acting on non-projected expression.

With dummy indices we can expand both spatial indices and non-spatial indices:

In[673]:=

cd[-a][W[a] W[b]]

Out[673]=

W_ ^b (D_a^ W_ ^a) + W_ ^a (D_a^ W_ ^b)

In[674]:=

cd[-a][V[b] V[-b]]

Out[674]=

In other cases, we prefer to show a warning and live the expression untouched:

In[675]:=

Catch @ cd[-a][V[a] V[b]]

Validate :: error : Induced derivative acting on non-projected expression.

The most important application of this in GR is the ADM-type decomposition of a spacetime. In the rest of this section we reproduce some equations from the well-organized notes on ADM by M. Choptuik.

1) Foliations and normals. We use his same notations for the normal vector and the acceleration vector:

In[676]:=

n[a] CD[-a][n[b]]//GradNormalToExtrinsicK//Expand

Out[676]=

An_ ^b

2) The projection tensor and the spatial metric. We do not follow the sign switch of York. The orthogonal projector is our pair Projectormetrich / ProjectWith[metrich] as explained above.

3) The spatial derivative operator and curvature tensor.

In[677]:=

cd[-a][metrich[-b, -c]]

Out[677]=

0

In[678]:=

(cd[-a] @ cd[-b][#] - cd[-b] @ cd[-a][#]) & @ W[-c]

Out[678]=

D_a^ D_b^ W_c^ - D_b^ D_a^ W_c^

In[679]:=

%//SortCovDs//ToCanonical

Out[679]=

R[D] _abcd^     W_ ^d

In[680]:=

Riemanncd[-a, -b, -c, d] {n[a], n[b], n[c], n[-d]}

Out[680]=

{0, 0, 0, 0}

In[681]:=

Riemanncd[-a, -c, -b, c]

Out[681]=

R[D] _ab^  

The contraction of Ricci into RicciScalar does not work:

In[682]:=

{Riccicd[-a, a], metrich[a, b] Riccicd[-a, -b], metricg[a, b] Riccicd[-a, -b]}

Out[682]=

{R[D] _^, R[D] _^, g_  ^ab R[D] _ab^  }

4) The extrinsic curvature tensor

In[683]:=

CD[-a][n[-b]]//GradNormalToExtrinsicK//ContractMetric

Out[683]=

-Kh_ab^   - An_b^ n_a^

In[684]:=

Antisymmetrize[ProjectWith[metrich][%], {-a, -b}]//ContractMetric//ToCanonical

Out[684]=

0

In[685]:=

ProjectWith[metrich][-1/2LieD[n[c], CD][metricg[-a, -b]]//GradNormalToExtrinsicK]//ContractMetric//ToCanonical

Out[685]=

Kh_ab^  

In[686]:=

-1/2LieD[n[c], CD][metrich[-a, -b]]//ProjectorToMetric//GradNormalToExtrinsicK//ContractMetric//ToCanonical

Out[686]=

Kh_ab^  

5) The Gauss-Codazzi equations. Single derivative:

In[687]:=

UndefTensor[v]

** UndefTensor: Undefined tensor v

In[688]:=

DefTensor[v[a], M3, OrthogonalTo→ {n[-a]}, ProjectedWith→ {metrich[-a, b]}]

** DefTensor: Defining tensor v[a] .

In[689]:=

CD[-c][v[-b]]

Out[689]=

▽_c^ v_b^

In[690]:=

%//ProjectWith[metrich]

Out[690]=

h_b ^( a) h_c ^( d) (▽_d^ v_a^ )

In[691]:=

%//ProjectorToMetric

Out[691]=

(δ_b ^( a) + n_ ^a n_b^ ) (δ_c ^( d) + n_c^ n_ ^d) (▽_d^ v_a^ )

In[692]:=

%//Expand

Out[692]=

n_ ^a n_c^ (▽_a^ v_b^ ) + n_ ^a n_b^ (▽_c^ v_a^ ) + ▽_c^ v_b^ + n_ ^a n_b^ n_c^ n_ ^d (▽_d^ v_a^ )

In[693]:=

%//GradNormalToExtrinsicK

Out[693]=

-n_b^ (-Kh_c ^( a) - An_ ^a n_c^ ) v_a^ - n_b^ n_c^ (-Kh_d ^( a) - An_ ^a n_d^ ) n_ ^d v_a^ + n_ ^a n_c^ (▽_a^ v_b^ ) + ▽_c^ v_b^

In[694]:=

%//Simplification

Out[694]=

Kh_ca^   n_b^ v_ ^a + n_ ^a n_c^ (▽_a^ v_b^ ) + ▽_c^ v_b^

We compare with expression (47) of Choptuik's notes:

In[695]:=

-% + CD[-c][v[-b]] - n[-b] v[-f] CD[-c][n[f]] + n[-c] n[e] CD[-e][v[-b]] - n[-c] n[-b] v[-f] Accelerationn[f]

Out[695]=

-Kh_ca^   n_b^ v_ ^a - An_ ^f n_b^ n_c^ v_f^ - n_ ^a n_c^ (▽_a^ v_b^ ) - n_b^ v_f^ (▽_c^ n_ ^f) + n_c^ n_ ^e (▽_e^ v_b^ )

In[696]:=

%//GradNormalToExtrinsicK

Out[696]=

-Kh_ca^   n_b^ v_ ^a - An_ ^f n_b^ n_c^ v_f^ - n_b^ (-Kh_c ^( f) - An_ ^f n_c^ ) v_f^ - n_ ^a n_c^ (▽_a^ v_b^ ) + n_c^ n_ ^e (▽_e^ v_b^ )

In[697]:=

%//Simplification

Out[697]=

0

Second derivatives. We correct Choptuik's equations (49) and (50), which are missing one term:

In[698]:=

ProjectWith[metrich][CD[-d][CD[-c][v[-b]]]] - cd[-d][cd[-c][v[-b]]]

Out[698]=

-(D_d^ D_c^ v_b^ ) + h_b ^( a) h_c ^( e) h_d ^( f) (▽_f^ ▽_e^ v_a^ )

In[699]:=

%//ProjectDerivative//ProjectDerivative

Out[699]=

-Underscript[P, h][▽_d^ Underscript[P, h][▽_c^ v_b^ ]] + h_b ^( a) h_c ^( e) h_d ^( f) (▽_f^ ▽_e^ v_a^ )

In[700]:=

%/.Projectormetrich→ProjectWith[metrich]

Out[700]=

-h_b ^( f) h_c ^( e) h_d ^( g) (▽_e^ v_a^ ) (▽_g^ h_f ^( a)) - h_b ^( a) h_c ^( f) h_d ^( g) (▽_e^ v_a^ ) (▽_g^ h_f ^( e))

In[701]:=

%//ProjectorToMetric//Expand

Out[701]=

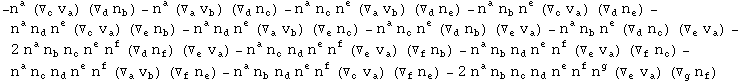
In[702]:=

%//GradNormalToExtrinsicK//Expand

Out[702]=

In[703]:=

%//ContractMetric

Out[703]=

Kh_c ^( a) Kh_db^   v_a^ - An_ ^a Kh_dc^   n_b^ v_a^ + Kh_dc^   n_ ^a (▽_a^ v_b^ )

In[704]:=

%//Simplification

Out[704]=

-An_ ^a Kh_cd^   n_b^ v_a^ + Kh_bd^   Kh_ca^   v_ ^a + Kh_cd^   n_ ^a (▽_a^ v_b^ )

First Gauss-Codazzi equation:

In[705]:=

expr1 = Projectormetrich[CD[-d][CD[-c][v[-b]]] - CD[-c][CD[-d][v[-b]]]]

Out[705]=

-Underscript[P, h][▽_c^ ▽_d^ v_b^ ] + Underscript[P, h][▽_d^ ▽_c^ v_b^ ]

In[706]:=

expr1A = expr1//SortCovDs

Out[706]=

Underscript[P, h][R[▽] _dcb ^(   a) v_a^ ]

In[707]:=

expr1/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[707]=

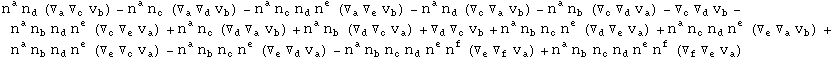
In[708]:=

expr1B = %//GradNormalToExtrinsicK//Simplification

Out[708]=

In[709]:=

expr2 = cd[-d][cd[-c][v[-b]]] - cd[-c][cd[-d][v[-b]]]

Out[709]=

-(D_c^ D_d^ v_b^ ) + D_d^ D_c^ v_b^

In[710]:=

expr2A = expr2//SortCovDs

Out[710]=

R[D] _dcb ^(   a) v_a^

In[711]:=

expr2//ProjectDerivative//ProjectDerivative

Out[711]=

-Underscript[P, h][▽_c^ Underscript[P, h][▽_d^ v_b^ ]] + Underscript[P, h][▽_d^ Underscript[P, h][▽_c^ v_b^ ]]

In[712]:=

%/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[712]=

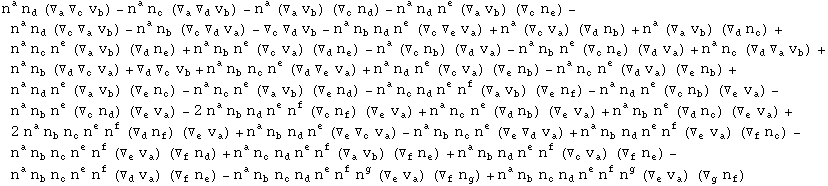
In[713]:=

%//GradNormalToExtrinsicK//ContractMetric

Out[713]=

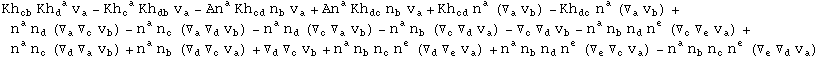
In[714]:=

expr2B = %//Simplification

Out[714]=

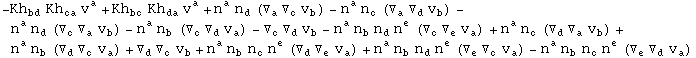
In[715]:=

(expr1A - expr1B) - (expr2A - expr2B)//Simplification

Out[715]=

In[716]:=

IndexSet[GCRiemann1[-a_, -b_, -c_, -d_], Simplification[(%/.v[_] →1//ScreenDollarIndices)]]

Out[716]=

Kh_ad^   Kh_bc^   - Kh_ac^   Kh_bd^   + Underscript[P, h][R[▽] _abcd^    ] - R[D] _abcd^    

If we decompose the Riemann tensor along the vector n

In[717]:=

inducedRiemann[-a_, -b_, -c_, -d_] = InducedDecomposition[RiemannCD[-a, -b, -c, -d], {metrich, n}]//ToCanonical

Out[717]=

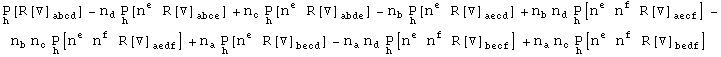
then we can express it as

In[718]:=

inducedRiemann[-a_, -b_, -c_, -d_] = inducedRiemann[-a, -b, -c, -d] - GCRiemann1[-a, -b, -c, -d]//ToCanonical

Out[718]=

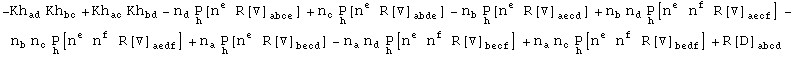
Second Gauss-Codazzi equation:

In[719]:=

expr1 = Projectormetrich[CD[-d][CD[-c][n[-b]]] - CD[-c][CD[-d][n[-b]]]]

Out[719]=

-Underscript[P, h][▽_c^ ▽_d^ n_b^ ] + Underscript[P, h][▽_d^ ▽_c^ n_b^ ]

In[720]:=

expr1A = expr1//SortCovDs

Out[720]=

Underscript[P, h][n_a^ R[▽] _dcb ^(   a)]

In[721]:=

expr1/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[721]=

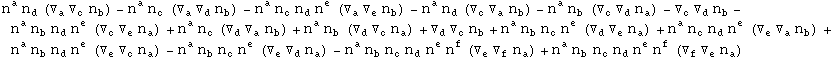
In[722]:=

expr1B = %//GradNormalToExtrinsicK//ContractMetric//GradNormalToExtrinsicK//Simplification

Out[722]=

In[723]:=

expr2A = cd[-c][ExtrinsicKmetrich[-b, -d]] - cd[-d][ExtrinsicKmetrich[-b, -c]]

Out[723]=

D_c^ Kh_bd^   - D_d^ Kh_bc^  

In[724]:=

expr2A//ProjectDerivative

Out[724]=

Underscript[P, h][▽_c^ Kh_bd^  ] - Underscript[P, h][▽_d^ Kh_bc^  ]

In[725]:=

%/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[725]=

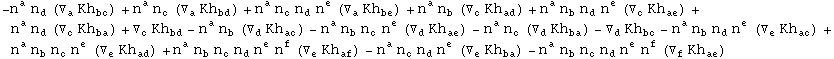
In[726]:=

expr2B = %//GradNormalToExtrinsicK//ContractMetric//Simplification

Out[726]=

In[727]:=

IndexSet[GCRiemann2[-b_, -c_, -d_], (expr1A - expr1B) - (expr2A - expr2B)//Simplification]

Out[727]=

-Underscript[P, h][n_ ^a R[▽] _bacd^    ] - D_c^ Kh_bd^   + D_d^ Kh_bc^  

We can further decompose the Riemann tensor now:

In[728]:=

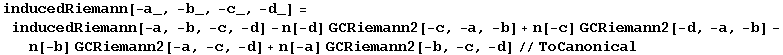
Out[728]=

"Third Gauss-Codazzi equation":

In[729]:=

expr1 = Projectormetrich[n[d] (CD[-d][CD[-c][n[-b]]] - CD[-c][CD[-d][n[-b]]])]

Out[729]=

Underscript[P, h][n_ ^d (-(▽_c^ ▽_d^ n_b^ ) + ▽_d^ ▽_c^ n_b^ )]

In[730]:=

expr1A = expr1//SortCovDs

Out[730]=

Underscript[P, h][n_a^ n_ ^d R[▽] _dcb ^(   a)]

In[731]:=

expr1/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[731]=

In[732]:=

expr1B = %//GradNormalToExtrinsicK//ContractMetric//GradNormalToExtrinsicK//Simplification

Out[732]=

-An_b^ An_c^ + Kh_b ^( d) Kh_cd^   + An_ ^d Kh_bd^   n_c^ - ▽_c^ An_b^ - n_c^ n_ ^d (▽_d^ An_b^ ) - n_ ^d (▽_d^ Kh_bc^  )

In[733]:=

expr2A = -cd[-c][Accelerationn[-b]] - Projectormetrich[n[d] CD[-d][ExtrinsicKmetrich[-b, -c]]]

Out[733]=

-Underscript[P, h][n_ ^d (▽_d^ Kh_bc^  )] - D_c^ An_b^

In[734]:=

expr2A//ProjectDerivative

Out[734]=

-Underscript[P, h][▽_c^ An_b^ ] - Underscript[P, h][n_ ^d (▽_d^ Kh_bc^  )]

In[735]:=

%/.Projectormetrich→ProjectWith[metrich]//ProjectorToMetric//Expand

Out[735]=

In[736]:=

expr2B = %//GradNormalToExtrinsicK//ContractMetric//Simplification

Out[736]=

An_ ^d Kh_bd^   n_c^ - ▽_c^ An_b^ - n_c^ n_ ^d (▽_d^ An_b^ ) - n_ ^d (▽_d^ Kh_bc^  )

Now we have (note that this pair of equations is equivalent to (105) of Choptuik):

In[737]:=

IndexSet[GCRiemann3[-b_, -c_], (expr1A - expr1B) - (expr2A - expr2B)//Simplification]

Out[737]=

An_b^ An_c^ - Kh_b ^( d) Kh_cd^   - Underscript[P, h][n_ ^a n_ ^d R[▽] _bdca^    ] + Underscript[P, h][n_ ^d (▽_d^ Kh_bc^  )] + D_c^ An_b^

In[738]:=

ProjectWith[metrich][LieD[n[a], CD][ExtrinsicKmetrich[-b, -c]] - n[a] CD[-a][ExtrinsicKmetrich[-b, -c]]//GradNormalToExtrinsicK]//Simplification//ContractMetric

Out[738]=

-2 Kh_b ^( a) Kh_ca^  

Finally we can combine the three Gauss-Codazzi equations into a single expression:

In[739]:=

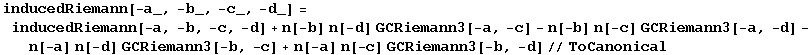
Out[739]=

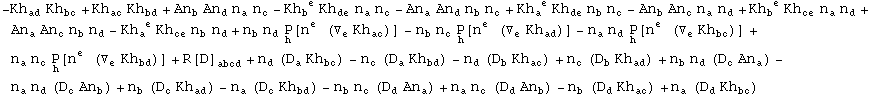
In[740]:=

GausCodazziRiemannRule = IndexRule[RiemannCD[-a, -b, -c, -d], inducedRiemann[-a, -b, -c, -d]]

Out[740]=

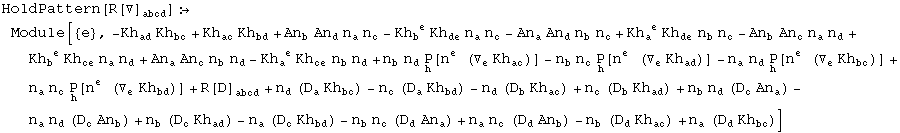
Most of the nontrivial computations in this area can now be easily performed using the Gauss-Codazzi formula. For example, let us compute the projections of the Ricci tensor and the Ricci scalar:

Decompose:

In[741]:=

inducedRicci[-a_, -b_] = InducedDecomposition[RicciCD[-a, -b], {metrich, n}]//NoScalar

Out[741]=

First formula:

In[742]:=

zero = RicciCD[-a, -b] - inducedRiemann[-a, -c, -b, -d] metricg[c, d]//ContractMetric//NoScalar

Out[742]=

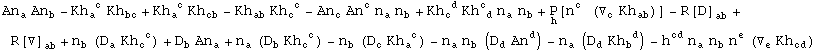
In[743]:=

zeroA = ProjectWith[metrich][%]//ContractMetric//ToCanonical

Out[743]=

An_a^ An_b^ - Kh_ab^   Kh_ ( c)^c + Underscript[P, h][n_ ^c (▽_c^ Kh_ab^  )] - R[D] _ab^   + h_a ^( c) h_b ^( d) R[▽] _cd^   + D_b^ An_a^

In[744]:=

zeroB = Projectormetrich[RicciCD[-a, -b]] - ProjectWith[metrich][RicciCD[-a, -b]]

Out[744]=

Underscript[P, h][R[▽] _ab^  ] - h_a ^( c) h_b ^( d) R[▽] _cd^  

In[745]:=

IndexSet[GCRicci1[-a_, -b_], zeroA + zeroB//ToCanonical]

Out[745]=

An_a^ An_b^ - Kh_ab^   Kh_ ( c)^c + Underscript[P, h][R[▽] _ab^  ] + Underscript[P, h][n_ ^c (▽_c^ Kh_ab^  )] - R[D] _ab^   + D_b^ An_a^

In[746]:=

inducedRicci[-a_, -b_] = inducedRicci[-a, -b] - GCRicci1[-a, -b]//ToCanonical

Out[746]=

Second formula:

In[747]:=

zero = (RicciCD[-a, -c] - inducedRiemann[-a, -b, -c, -d] metricg[b, d]) n[c]//ContractMetric//NoScalar

Out[747]=

In[748]:=

zeroA = ProjectWith[metrich][%]//MetricToProjector//ToCanonical

Out[748]=

h_a ^( c) n_ ^b R[▽] _bc^   - D_a^ Kh_ ( b)^b + D_b^ Kh_a ^( b)

In[749]:=

zeroB = Projectormetrich[RicciCD[-a, -b] n[b]] - ProjectWith[metrich][RicciCD[-a, -b] n[b]]

Out[749]=

Underscript[P, h][n_ ^b R[▽] _ab^  ] - h_a ^( c) n_ ^b R[▽] _cb^  

In[750]:=

IndexSet[GCRicci2[-a_], zeroA + zeroB//ToCanonical]

Out[750]=

Underscript[P, h][n_ ^b R[▽] _ab^  ] - D_a^ Kh_ ( b)^b + D_b^ Kh_a ^( b)

In[751]:=

inducedRicci[-a_, -b_] = inducedRicci[-a, -b] + GCRicci2[-a] n[-b] + GCRicci2[-b] n[-a]//ToCanonical

Out[751]=

Third formula:

In[752]:=

zero = (RicciCD[-a, -c] - inducedRiemann[-a, -b, -c, -d] metricg[b, d]) n[a] n[c]//Expand//ReplaceDummies

Out[752]=

In[753]:=

inducedRicci[-a_, -b_] = inducedRicci[-a, -b] - n[-a] n[-b] zero//Expand//SameDummies

Out[753]=

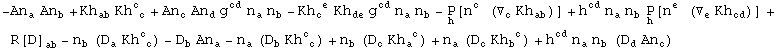
Finally, the Ricci scalar:

In[754]:=

inducedRiemann[-a, -b, -c, -d] metricg[b, d] metricg[a, c]//ContractMetric//NoScalar

Out[754]=

In[755]:=

%/.Projectormetrich→ProjectWith[metrich]//ContractMetric//ToCanonical

Out[755]=

-2 An_a^ An_ ^a + Kh_ab^   Kh_  ^ab + Kh_ ( a)^a Kh_ ( b)^b + R[D] _^ - 2 (D_a^ An_ ^a) - 2 h_  ^bc n_ ^a (▽_a^ Kh_bc^  )

In[756]:=

%//ProjectorToMetric//ContractMetric

Out[756]=

In[757]:=

%//GradNormalToExtrinsicK

Out[757]=

-2 An_a^ An_ ^a + Kh_ab^   Kh_  ^ab + Kh_ ( a)^a Kh_ ( b)^b + R[D] _^ - 2 (D_a^ An_ ^a) - 2 n_ ^a (▽_a^ Kh_b ^( b))

With a lapse:

In[758]:=

inducedRicciScalar[] = %/.LapseRule//Expand

Out[758]=

Kh_ab^   Kh_  ^ab + Kh_ ( a)^a Kh_ ( b)^b + R[D] _^ - (2 (D_a^ D_ ^aα_^))/α_^ - 2 n_ ^a (▽_a^ Kh_b ^( b))

In[759]:=

UndefMetric[metrich]

** UndefTensor: Undefined antisymmetric tensor epsilonmetrich

** UndefTensor: Undefined symmetric Christoffel tensor Christoffelcd

** UndefTensor: Undefined symmetric Einstein tensor Einsteincd

** UndefTensor: Undefined symmetric Ricci tensor Riccicd

** UndefTensor: Undefined Ricci scalar RicciScalarcd

** UndefTensor: Undefined Riemann tensor Riemanncd

** UndefTensor: Undefined symmetric TFRicci tensor TFRiccicd

** UndefTensor: Undefined vanishing torsion tensor Torsioncd

** UndefTensor: Undefined vanishing Weyl tensor Weylcd

** UndefCovD: Undefined covariant derivative cd

** UndefTensor: Undefined extrinsic curvature tensor ExtrinsicKmetrich

** UndefTensor: Undefined acceleration vector Accelerationn

** UndefInertHead: Undefined projector inert-head Projectormetrich

** UndefTensor: Undefined symmetric metric tensor metrich

In[760]:=

UndefTensor/@{V, W} ;

** UndefTensor: Undefined tensor V

** UndefTensor: Undefined tensor W

Created by Mathematica  (May 16, 2008) Valid XHTML 1.1!