7.10. Variational derivatives
There is not yet a concept of integration in xTensor`. Instead of working with a variational derivative of a functional, we shall assume that such a functional is the integral of some integrand (or "Lagrangian") and that the integral is computed with respect to a volume form which vanishes under the action of some derivative (this is the derivative which will be "integrated by parts").
Let us fake the presence of a scalar density:
In[761]:=
![]()
![]()
We need only these two properties:
In[762]:=
![]()
In[763]:=
![]()
For instance, let us compute the RicciScalar field of our metric:
In[764]:=
![]()
Out[764]=
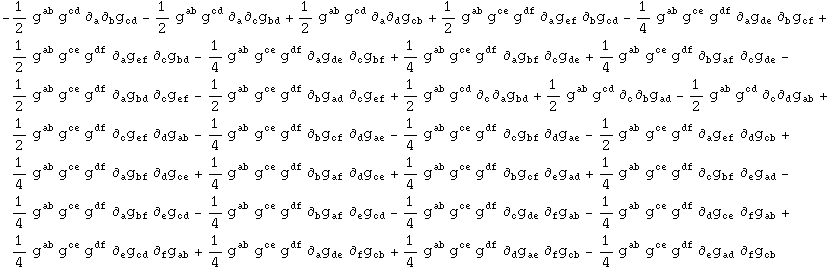
Working intensively with partial derivatives, it is interesting to set
In[765]:=
![]()
Out[765]=
![]()
Now we perform a direct variational derivative of the Einstein-Hilbert Lagrangian with respect to the inverse metric. It is a long computation, producing 501 terms:
In[766]:=
![]()
Out[766]=
![]()
The expected result is the Einstein tensor:
In[767]:=
![]()
Out[767]=
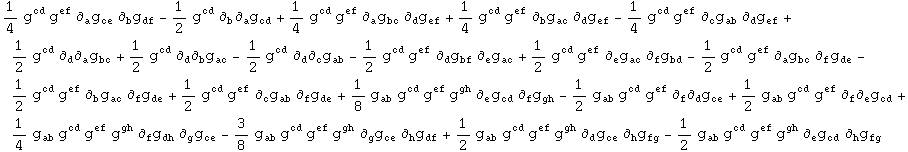
In[768]:=
![]()
Out[768]=
![]()
Let us now define the electromagnetic fields:
In[769]:=
![]()
![]()
In[770]:=
![]()
![]()
In[771]:=
![]()
This is the electromagnetic Lagrangian:
In[772]:=
![]()
Out[772]=
![]()
and these are the Maxwell equations on a curved background:
In[773]:=
![]()
Out[773]=
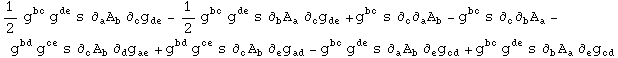
In[774]:=
![]()
Out[774]=
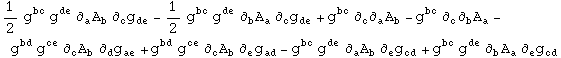
In[775]:=
![]()
Out[775]=
![]()
In[776]:=
![]()
![]()
![]()
![]()
Restore standard options:
In[777]:=
![]()
Out[777]=
![]()
| Created by Mathematica (May 16, 2008) |