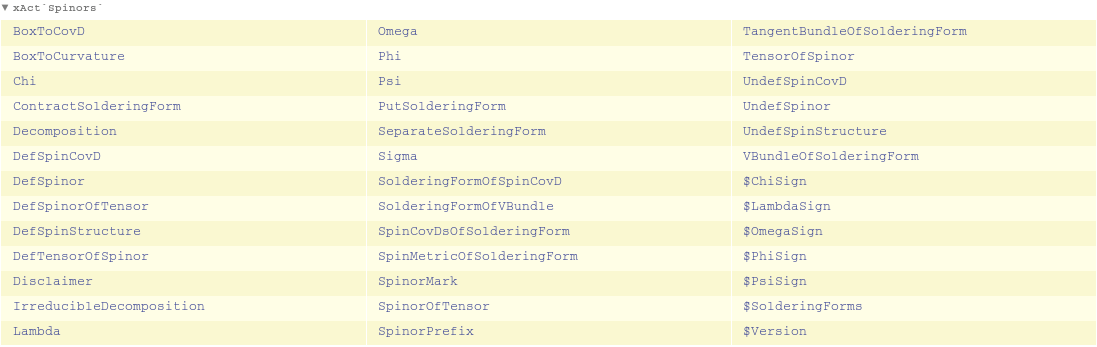
This is the doc file SpinorsDoc.nb of version 0.9.2 of Spinors`. Last update on 9 September 2009.
Authors
© 2006-2009, under the GNU General Public License (GPL)
Alfonso García-Parrado Gómez-Lobo
Centro de Matematica
Universidade do Minho, Portugal
algar@mai.liu.se
and
José M. Martín-García
Institut d'Astrophysique de Paris & Laboratoire Univers et Théories, CNRS, France
garcia@iap.fr
http://metric.iem.csic.es/Martin-Garcia/
Intro
Spinors` is the xAct` package for computations with spinors in four dimensional Lorentzian manifolds. The conventions adopted in the standard formulae of the spinor calculus are those of Penrose & Rindler, Spinors and Space-Time, Cambridge University Press (Vols. 1, 2). We assume that the user is already familiar with spinor calculus and therefore we will not explain the terminology or symbols related to this subject unless necessary to clarify the workings of the package.
Load the package
This loads the package from the default directory, for example $Home/.Mathematica/Applications/xAct/ for a single-user installation under Linux.
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
<<xAct`Spinors`
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Comparing, we see that all packages take about 50 Mb in Mathematica 7.0:
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
There are several contexts: xAct`Spinors`, xAct`xTensor`, xAct`xPerm` and xAct`xCore` contain the respective reserved words. System` contains Mathematica's reserved words. The current context Global` will contain your definitions and right now is empty.
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
![]()
In[7]:=
![]()
![]()
1. Example session
Spinors are elements of a complex vector bundle (spin bundle) whose base space is a four dimensional Lorentzian manifold (spacetime). Therefore we need to define first a four dimensional differentiable manifold and a Lorentzian metric, which will be kept fixed in all this notebook. See xTensor` doc file for details about how to carry this out. Note also that all the tools and notation developed in xAct` to work with generic complex vector bundles apply in the particular case of a spin bundle, so the user will be assumed familiar with them. We refer again to the xTensor` doc file for detailed documentation about this point.
Definition of a four dimensional manifold M4:
In[8]:=
![]()
![]()
![]()
Definition of a Lorentzian metric on the manifold:
In[9]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The command DefSpinStructure defines a complex spin bundle named Spin comprising the spin metric ε[-A,-B], the soldering form σ[a,-A,-A†]and the extension of the Levi-Civita covariant derivative CD to the unique covariant derivative CDe which is compatible with the soldering form and the spin metric (spin covariant derivative). The option SpinorPrefix is used to introduce a tag which will be prepended automatically to any spinor related to a spacetime tensor.
In[10]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
When a spin structure is defined, several new objects are defined automatically. These are the spinor equivalents of the Riemann, the Ricci, the traceless Ricci and the Weyl tensors. Note the character σ prepended to each head in the output . This is the default output form of the tag mentioned above. This output form can be changed with the option SpinorMark in the command DefSpinStructure.
In[11]:=
![]()
Out[11]=
![]()
The curvature spinors are also automatically defined.
In[12]:=
![]()
Out[12]=
![]()
Each of the above spinors can be decomposed into irreducible parts by means of the command Decomposition. Let us see some examples.
In[13]:=
![]()
Out[13]=
![]()
The decomposition of the spinor equivalent of the Ricci tensor is
In[14]:=
![]()
Out[14]=
![]()
The decomposition of the spinor equivalent of the Weyl tensor is
In[15]:=
![]()
Out[15]=
![]()
The inner curvature of the spin bundle can be also decomposed according to standard rules .
In[16]:=
![]()
Out[16]=
![]()
In[17]:=
![]()
Out[17]=
![]()
In[18]:=
![]()
Out[18]=
![]()
In[19]:=
![]()
Out[19]=
![]()
Spinors` is able to work with the 2-index derivatives used in spinor calculus.
In[20]:=
![]()
Out[20]=
![]()
As is well-known this is nothing but a shorthand for
In[21]:=
![]()
Out[21]=
![]()
We can also transform one-index covariant derivatives back into their two index form by means of the soldering form.
In[22]:=
![]()
Out[22]=
![]()
In[23]:=
![]()
Out[23]=
![]()
In[24]:=
![]()
Out[24]=
![]()
Spinors are defined using the command DefSpinor, which is nothing but a renaming of standard xAct` command DefTensor (by default the option Dagger->Complex is assumed).
In[25]:=
![]()
![]()
![]()
In this case the spinor just defined can be related to a tensor in the spacetime tangent bundle. This vector is given by
In[26]:=
![]()
Out[26]=
![]()
The soldering form can be absorbed into the spinor κ. In this case a new tensor is automatically defined.
In[27]:=
![]()
![]()
![]()
![]()
Out[27]=
![]()
The original spinor may be also recovered from ![]() .
.
In[28]:=
![]()
Out[28]=
![]()
In[29]:=
![]()
Out[29]=
![]()
An interesting feature is the possibility of working with Hermitian spinors. These are defined by supplying the option Dagger->Hermitian to DefSpinor.
In[30]:=
![]()
![]()
![]()
We check that the new spinor μ is hermitian.
In[31]:=
![]()
Out[31]=
![]()
Any Hermitian spinor has a tensor counterpart which is real. We compute the tensor counterpart of μ and check that the result is a real rank-2 spacetime tensor.
In[32]:=
![]()
![]()
![]()
Out[32]=
![]()
In[33]:=
![]()
Out[33]=
![]()
The xAct` command ContractMetric is aware of the standard index raising and lowering conventions for the spinor indices and therefore it can act on spinor expressions without further options. We present some examples:
In[34]:=
![]()
![]()
![]()
We consider the following list of quantities.
In[35]:=
![]()
Out[35]=
![]()
In[36]:=
![]()
Out[36]=
![]()
The same goes for the remaining xAct` commands. For example ToCanonical takes into account the "see-saw" rule when canonicalising spinor expressions and adds the suitable signs. Also it works with any kind of spinor expression without any further option. To see this let us canonicalise the following list of spinor expressions.
In[37]:=
![]()
Out[37]=
![]()
In[38]:=
![]()
Out[38]=
![]()
A spin structure can be undefined and all its dependent symbols are thus removed from the session. To accomplish this we remove first all the visitors of the soldering form σ:
In[39]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
and all the objects defined on the Spin vbundle :
In[40]:=
![]()
Out[40]=
![]()
In[41]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Finally the spin structure and all its dependent objects are removed.
In[42]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now, we are only left with spacetime quantities.
In[43]:=
![]()
Out[43]=
![]()
2. Definition of a spin structure
In our present context we need the following ingredients to introduce a spin structure on a Lorentzian manifold: a 2-dimensional complex vector bundle (the spin bundle), the antisymmetric spin metric and the soldering form. This last quantity is a mixed object having indices in the spin bundle and the tangent bundle and serves to relate space-time quantities to spinor quantities and back (see e. g. appendix A of A. Ashtekar Lectures on non-perturbative canonical gravity World Scientific, Singapore, 1991). The explicit components of the soldering form in a basis are known as the Infeld-Van der Waerden symbols. It can be shown that there exists a unique covariant derivative (spin covariant derivative) which is compatible with both the spin metric and the soldering form. The restriction of the spin covariant derivative to tensors defined on the tangent bundle coincides with the Levi-Civita covariant derivative.
It is possible to introduce a spin structure both in a spacetime with or without torsion. We separate those two cases:
2.1. Spin structures on spacetimes without torsion
To define a spin structure we need first a four dimensional Lorentzian manifold
In[44]:=
![]()
Out[44]=
![]()
DefSpinStructure Define a spin structure on a four dimensional Lorentzian manifold.
UndefSpinStructure Undefine a spin structure.
$SolderingForms List of soldering forms (a.k.a. spin structures).
We define a spin structure comprising the complex vector bundle Spin whose abstract indices are {A, B, C, D, F, H, L, P, Q}. We need to supply as arguments the name of the metric tensor of the background Lorentzian manifold g[-a,-b], the name of the antisymmetric spin metric ε[-A,-B], the name of the soldering form σ[a,-A,-A†] and the name of the spin covariant derivative CDe[-a].The option SpinorPrefix is used to introduce a tag which will be prepended automatically to any spinor related to a spacetime tensor and the option SpinorMark introduces a formatting of the tag SP different to the default one. The long output of DefSpinStructure can be suppressed by adding the option Info->False which deactivates the information of the definition commands .
In[45]:=
![]()
![]()
![]()
We choose a formatting for the "primed" spinor indices according to the standard conventions used in the literature.
In[46]:=
![]()
By convention we choose the symbol σ as the representative of all the elements which comprise the spin structure. Hence it will sometimes be referred to as "the spin structure". In particular this means that it is the host of the spinor counterparts of the metric tensor, the volume element and all the curvature spinors associated to the covariant derivative CDe .
In[47]:=
![]()
Out[47]=
![]()
The set of soldering forms is kept in the global variable $SolderingForms.
In[48]:=
![]()
Out[48]=
![]()
All the essential algebraic properties of the soldering form are included as automatic rules. Example:
In[49]:=
![]()
Out[49]=
![]()
It is possible to define a second spin structure on the manifold M4.
In[50]:=
![]()
In[51]:=
![]()
Out[51]=
![]()
If we have more than one spin structure in the session then we need to specify which one are we working with in some of the Spinors` commands. Otherwise it is automatically assumed that we work with the default spin structure which is the first element of the list $SolderingForms.Examples:
In[52]:=
![]()
Out[52]=
![]()
In[53]:=
![]()
Out[53]=
![]()
In[54]:=
![]()
Out[54]=
![]()
In[55]:=
![]()
Out[55]=
![]()
In[56]:=
![]()
Out[56]=
![]()
In[57]:=
![]()
Out[57]=
![]()
In[58]:=
![]()
Out[58]=
![]()
We remove the spin structure σ2. As usual, we start with the visitors of σ2 and then we proceed to erase the spin structure itself.
In[59]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[60]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.2. Spin structures on spacetimes with torsion
It is possible to define a spin structure on a spacetime in which the connection compatible with the metric tensor is assumed to have torsion. In this section we illustrate this.
We need to define a new 4-dimensional manifold and a new metric. Note the non-standard symmetry properties of the curvature tensors:
In[61]:=
![]()
![]()
![]()
In[62]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Definition of the spin structure
In[63]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This is the torsion tensor.
In[64]:=
![]()
Out[64]=
![]()
We compute next the spinor equivalent of the torsion.
In[65]:=
![]()
Out[65]=
![]()
In[66]:=
![]()
Out[66]=
![]()
This can be decomposed as follows.
In[67]:=
![]()
Out[67]=
![]()
In[68]:=
![]()
Out[68]=
![]()
The spinor ![]() is called the "torsion spinor" of the covariant derivative. It is symmetric in the last pair of indices.
is called the "torsion spinor" of the covariant derivative. It is symmetric in the last pair of indices.
In[69]:=
![]()
Out[69]=
![]()
That spinor appears in all standard expressions involving the torsion. Let us see an example:
In[70]:=
![]()
![]()
![]()
This is the spinor form of the Ricci identity associated to the covariant derivative cde. As is well known this spinor form contains the "box operator" whose expansion contains explicitly the torsion spinor.
In[71]:=
![]()
Out[71]=
![]()
In[72]:=
![]()
Out[72]=
![]()
We remove all the symbols used in this subsection.
In[73]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[74]:=
![]()
![]()
![]()
In[75]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[76]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
In[77]:=
![]()
![]()
![]()
In[78]:=
![]()
Out[78]=
![]()
3. Transformation between spinor and tensor expressions
Being able to transform spinor expressions into tensor ones and back is an important issue. Sometimes this is a trivial task but there are cases in which more efforts are required. Spinors` has a complete suite of commands which enable us to handle any case as we show below.
3.1. Insertion and removal of soldering forms in an expression
When transforming a spinor expression into a tensor one (or vice-versa) we may need to insert or eliminate a number of soldering forms. Spinors` provides commands to perform this task in an efficient fashion.
PutSolderingForm Contraction of spinor/tensor indices with a suitable number of soldering forms
ContractSolderingForm Transformation of contracted products of soldering forms into tensor/spinor expressions
SeparateSolderingForm Extraction of spinor/tensor indices by means of soldering forms
Simple application: we start with the Riemann tensor and finish with its spinor counterpart
In[79]:=
![]()
Out[79]=
![]()
In[80]:=
![]()
Out[80]=
![]()
In[81]:=
![]()
Out[81]=
![]()
We can now follow previous procedure backwards and end up in the spacetime Riemann tensor.
In[82]:=
![]()
Out[82]=
![]()
In[83]:=
![]()
Out[83]=
![]()
Sometimes intermediate objects need to be created in a computation like the one just shown. This is done by the system in an automatic way.
In[84]:=
![]()
![]()
In[85]:=
![]()
Out[85]=
![]()
Here, the contraction of the soldering forms results in the spinor counterpart of the tensor M[-a, -b]. The former has not been defined previously and thus the system must introduce this new object (a message informing about this is issued). The definition of spinor counterparts of tensor objects can be performed by the user independently (see next section).
In[86]:=
![]()
![]()
![]()
![]()
Out[86]=
![]()
The separation of the soldering form gets us back to the original tensor ![]() .
.
In[87]:=
![]()
Out[87]=
![]()
In[88]:=
![]()
Out[88]=
![]()
The spinors SP—M and SP—M† are visitors of M. Therefore if we wish to remove M, we need to remove first its visitors.
In[89]:=
![]()
![]()
![]()
In[90]:=
![]()
![]()
There are cases in which we need to tell explicitly how the indices of the soldering forms should be contracted when they act on an expression. This is achieved by means of extra options in the commands just ilustrated.
Consider an expression containing spacetime and spinor indices.
In[91]:=
![]()
Out[91]=
![]()
By default SeparateSolderingForm will extract soldering forms from all the tensor indices and all the complex conjugated pairs of spinor indices.
In[92]:=
![]()
Out[92]=
![]()
We may control with extra options the vector bundles whose indices will be pulled out by SeparateSolderingForm.
In[93]:=
![]()
Out[93]=
![]()
In[94]:=
![]()
Out[94]=
![]()
A similar index-selection is also available for PutSolderingForm.
In[95]:=
![]()
Out[95]=
![]()
In[96]:=
![]()
Out[96]=
![]()
The following expression is the spinor form of a tensor (Bel-Robinson tensor). If we wish to use PutSolderingForm to find its tensor equivalent we need to pass an argument stating how the spinor indices are grouped into tensor ones as there is not a unique way of doing it. This is achieved by means of the head Pair which represents conjugated pairs of spinor indices.
In[97]:=
![]()
Out[97]=
![]()
In[98]:=
![]()
Out[98]=
![]()
3.2. Relations between spinors and tensors
There are spinors which can be put into relation with tensors and tensors which can be put into relation with spinors. In both cases the relation is carried out by means of the soldering form. Whenever one of these relations apply, Spinors` enables the user to define the spinor (resp. tensor) counterpart of a tensor (resp. spinor).
DefSpinorOfTensor Defines the spinor counterpart of a tensor (when applicable)
DefTensorOfSpinor Defines the tensor counterpart of a spinor (when applicable)
Let us define a spinor.
In[99]:=
![]()
![]()
![]()
This spinor has a tensor counterpart. To introduce it into the session we use the command DefTensorOfSpinor in the following way:
In[100]:=
![]()
![]()
![]()
The output form of the tensor is actually constructed from that of the spinor:
In[101]:=
![]()
Out[101]=
![]()
The symbol KT represents the tensor counterpart of the spinor κ.This must be a symbol which does not correspond to any object defined previously in the session. From this point on, the system stores KT as the tensor counterpart of κ. Any of the commands which relate spinors to tensors are now aware of this binding between κ and KT.Let us see some examples:
In[102]:=
![]()
Out[102]=
![]()
We start from the spinor ![]() transform it into a tensor and then back to the same spinor all by using PutSolderingForm/ContractSolderingForm.
transform it into a tensor and then back to the same spinor all by using PutSolderingForm/ContractSolderingForm.
In[103]:=
![]()
Out[103]=
![]()
In[104]:=
![]()
Out[104]=
![]()
In[105]:=
![]()
Out[105]=
![]()
In[106]:=
![]()
Out[106]=
![]()
In[107]:=
![]()
Out[107]=
![]()
Similarly we can introduce the spinor counterpart of any tensor already defined in the sesssion. For example:
In[108]:=
![]()
![]()
![]()
In[109]:=
![]()
![]()
![]()
As above the symbol ST should not correspond to any of the symbols defined previously in the session. Note carefully the index arrangement in the spinor ST. This is fixed by convention and cannot be altered by the user. We will come back to this important point below. For now we present some manipulation examples.
In[110]:=
![]()
Out[110]=
![]()
In[111]:=
![]()
Out[111]=
![]()
In[112]:=
![]()
Out[112]=
![]()
In[113]:=
![]()
Out[113]=
![]()
In[114]:=
![]()
Out[114]=
![]()
In[115]:=
![]()
Out[115]=
![]()
The above examples can be generalized to tensors and spinors with a higher number of indices with the following provision: in the commands DefSpinorOfTensor and DefTensorOfSpinor spinor indices must be always arranged according to the pattern index-Dagger[index]. Otherwise an error message is thrown.
In[116]:=
![]()
![]()
In[117]:=
![]()
![]()
![]()
In[118]:=
![]()
![]()
We undefine the objects used in this subsection. Note that whenever we wish to undefine a spinor (tensor) quantity with a tensor (spinor) counterpart we must erase first the latter, which is a visitor of the former.
In[119]:=
![]()
![]()
![]()
In[120]:=
![]()
![]()
![]()
In[121]:=
![]()
![]()
![]()
In[122]:=
![]()
![]()
![]()
In[123]:=
![]()
![]()
![]()
3.3. Products of soldering forms
Contracted products of soldering forms appear in a natural way when transforming spinor expressions into tensor ones and back. Therefore it is important to be able to work with such products. In this subsection we show how Spinors` deals with such quantities.
The simplest case is the product of 2 soldering forms which gives rise to an auxiliary quantity which is needed when going from spinor expressions to tensor expressions.
In[124]:=
![]()
Out[124]=
![]()
The algebraic properties of ![]() are stored as automatic rules.
are stored as automatic rules.
In[125]:=
![]()
Out[125]=
![]()
In[126]:=
![]()
|
|||||||||||||||||||||||||||||||||
One of the previous properties is that the "square" of ![]() gives rise to the "tetra-metric". The latter is a four rank spacetime tensor which is defined in eq. (3.4.57) of vol. 1 of Penrose & Rindler (note that they use the name U for it).
gives rise to the "tetra-metric". The latter is a four rank spacetime tensor which is defined in eq. (3.4.57) of vol. 1 of Penrose & Rindler (note that they use the name U for it).
In[127]:=
![]()
Out[127]//InputForm=
-Tetrag[-d, -b, -a, -c]
This is the explicit definition of the tetra-metric (note that there is a sign difference between formula (3.4.57) of Vol. 1of Penrose & Rindler and our formula).
In[128]:=
![]()
Out[128]=
![]()
As we can see the tetra-metric only depends on spacetime quantities. Therefore the tetra-metric is always automatically defined whenever a Lorentzian four dimensional metric is introduced regardless to whether a spin structure has been defined. Also automatic rules implementing the algebraic properties of the tetra-metric are stored.
In[129]:=
![]()
|
A typical problem is the computation of a product of soldering forms with no free spinor indices. These always give rise to contracted products of tetra metrics. Let us see some examples.
In[130]:=
![]()
Out[130]=
![]()
In[131]:=
![]()
Out[131]=
![]()
In[132]:=
![]()
Out[132]=
![]()
In[133]:=
![]()
Out[133]=
![]()
Expressions of the sort just found are frequent in computations involving the transformation of spinor expressions into tensor ones. Let us see an example
Transformation of the Weyl tensor into its spinor counterpart
In[134]:=
![]()
Out[134]=
![]()
In[135]:=
![]()
Out[135]=
![]()
In[136]:=
![]()
Out[136]=
![]()
This spinor expression can be transformed back into the Weyl tensor
In[137]:=
![]()
Out[137]=
![]()
We use this expression to write the Weyl spinor ![]() in terms of the Weyl tensor
in terms of the Weyl tensor ![]() .
.
In[138]:=
![]()
Out[138]=
![]()
In[139]:=
![]()
Out[139]=
![]()
In[140]:=
![]()
Out[140]=
![]()
In[141]:=
![]()
Out[141]=
![]()
Now we can use previous rule to find the tensor expression of any invariant written in terms of the Weyl spinor. For example consider
In[142]:=
![]()
Out[142]=
![]()
A direct use of ContractSolderingForm would contract the soldering forms with the Weyl tensor, yielding an undesired result:
In[143]:=
![]()
Out[143]=
![]()
Instead we specify contraction of the indices on the soldering form which are dummies, generating a product of "tetra-metrics".
In[144]:=
![]()
Out[144]=
![]()
In[145]:=
![]()
Out[145]=
![]()
Finally we expand the tetra-metrics into ordinary metrics and volume elements. The simplification of the resulting expression provides the final answer.
In[146]:=
![]()
Out[146]=
![]()
In[147]:=
![]()
Out[147]=
![]()
Clean up :
In[148]:=
![]()
4. Decomposition of a spinor into irreducible parts
A classical result of the spinor algebra is the posibility of decomposing any spinor into a sum which consists of a totally symmetric spinor of the same rank as the given spinor plus other terms which are outer products of the antisymmetric metric with totally symmetric spinors of lower rank (see proposition 3.3.54 of Penrose & Rindler vol. I for full details). In Spinors` there is an automated procedure to find such a decomposition as we explain below.
IrreducibleDecomposition Finds the decomposition of any spinor into irreducible parts
We show how IrreducibleDecomposition works by means of some simple examples. Let us start by defining a spinor
In[149]:=
![]()
![]()
![]()
The decomposition of the spinor just introduced into irreducible parts is given by
In[150]:=
![]()
![]()
![]()
Out[150]=
![]()
The command IrreducibleDecomposition defines first the totally symmetric spinors intervening in the decomposition (irreducible spinors). The actual decomposition is found in a second step and displayed in the output. In order to represent the irreducible spinors, we introduce an indexed quantity with a variable number of slots (see the documentation of the package xTensor` for further details about this). Note the labels on each of the totally symmetric spinors: these are label indices which are used to distinguish each of the irreducible spinors. The pairs of numbers which appear inside the list indicate which slots of the tensor being decomposed have been picked to "pull out" factors of the antisymmetric metric.
This is the list of all the irreducible spinors resulting from the decomposition of Kh[-A, -B, -C, -D].
In[151]:=
![]()
Out[151]=
![]()
The symbol TF (trace free) is prepended to the symbol Kh. All the quantities of the previous list which are not scalars are totally symmetric.
In[152]:=
![]()
Out[152]=

The irreducible spinors are servants of the spinor they decompose. Therefore they are removed if the latter is erased.
In[153]:=
![]()
![]()
![]()
![]()
![]()
Example of the decomposition of a mixed spinor.
In[154]:=
![]()
![]()
![]()
Out[154]=
![]()
5. Spin-compatible covariant derivatives
Spinors` includes the concept of spin-compatible covariant derivative. A covariant derivative is spin-compatible if it yields zero when acting upon a soldering form. The spin covariant derivative which extends the Levi-Civita covariant derivative is an example of it.
DefSpinCovD Defines a spin-compatible covariant derivative
UndefSpinCovD Undefines a spin-compatible covariant derivative
We define a covariant derivative which is spin-compatible with the soldering form σ. Note that the syntax of DefSpinCovD is similar to the xAct` command DefCovD used to define covariant derivatives. We use non-standard symbols to denote the derivative:
In[155]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Several new objects are defined along with the covariant derivative. These are the same which are introduced by DefCovD plus the spinor equivalents of all the curvature quantities. By definition the compatibility of the covariant derivative nb with the spin structure associated to σ means that
In[156]:=
![]()
Out[156]=
![]()
Rules to decompose the curvature spinors into irreducible parts are also available. For example, let us compute the full decomposition of the spinor counterpart of the Riemann tensor of the covariant derivative nb in irreducible parts.
In[157]:=
![]()
Out[157]=
![]()
In[158]:=
![]()
Out[158]=
![]()
In[159]:=
![]()
Out[159]=
![]()
In[160]:=
![]()
Out[160]=
![]()
In[161]:=
![]()
Out[161]=
![]()
Note that the curvature spinors associated to a generic spin-compatible covariant derivative do not have the same symmetries as those of the spin covariant derivative.
In[162]:=
![]()
Out[162]=
![]()
There are also decomposition rules for the torsion spinor.
In[163]:=
![]()
Out[163]=
![]()
In[164]:=
![]()
Out[164]=
![]()
In[165]:=
![]()
Out[165]=
![]()
In[166]:=
![]()
Out[166]=
![]()
The covariant derivative nb can be manipulated in 2-index or in single index notation.
In[167]:=
![]()
Out[167]=
![]()
In[168]:=
![]()
Out[168]=
![]()
In[169]:=
![]()
Out[169]=
![]()
In postfix notation :
In[170]:=
![]()
In[171]:=
![]()
Out[171]=
![]()
In[172]:=
![]()
The spinor expression of the Ricci identities of any spin-compatible covariant derivative is neatly rendered in terms of the box operator. This is a linear differential operator and Spinors` is able to work with it. The box operator is represented by the head BoxCovDname where the symbol CovDname represents the spin-compatible covariant derivative.
Action of the box operator on a spinor and some simple manipulations involving it.
In[173]:=
![]()
![]()
![]()
In[174]:=
![]()
Out[174]=
![]()
In[175]:=
![]()
Out[175]=
![]()
In[176]:=
![]()
Out[176]=
![]()
In[177]:=
![]()
Out[177]=
![]()
The box operator can be expanded into spin covariant derivatives or into curvature spinors plus the torsion, according to known formulae (see eqs. (4.9.8)-(4.9.17) of Penrose & Rindler Vol. 2). Spinors has built-in rules to perform these expansions.
BoxToCovD Expand the box operator into covariant derivatives
BoxToCurvature Expand the box operator into curvature spinors
Examples of the expansion of the Box operator.
In[178]:=
![]()
Out[178]=
![]()
In[179]:=
![]()
Out[179]=
![]()
In[180]:=
![]()
Out[180]=
![]()
Similar computations for the box operator arising from the covariant derivative nb. Note the presence of an extra term due to the fact that the covariant derivative nb has torsion.
In[181]:=
![]()
Out[181]=
![]()
In[182]:=
![]()
Out[182]=
![]()
In[183]:=
![]()
Out[183]=
![]()
Other computations involving the box operator.
In[184]:=
![]()
Out[184]=
![]()
In[185]:=
![]()
Out[185]=
![]()
In[186]:=
![]()
Out[186]=
![]()
In[187]:=
![]()
Out[187]=
![]()
In[188]:=
![]()
Out[188]=
![]()
In[189]:=
![]()
Out[189]=
![]()
We no longer need the spin-compatible covariant derivative nb :
In[190]:=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Example: Killing spinors
Let us introduce a symmetric valence-2 spinor:
In[191]:=
![]()
![]()
![]()
We will say that the spinor ![]() is a Killing spinor if the following differential condition is fulfilled.
is a Killing spinor if the following differential condition is fulfilled.
In[192]:=
![]()
Out[192]=
![]()
In[193]:=
![]()
Killing spinors have a number of applications. For example whenever a Killing spinor exists then automatically one can construct a conformal Killing-Yano tensor and a conformal Killing spinor in the spacetime which in turn lead to the existence of integration constants for the geodesic equations. These results were presented by M. Walker and R. Penrose in "On Quadratic First Integrals of the Geodesic Equations in {2,2} Spacetimes" Comm. Math. Phys. 18 265-274 (1970) and we will re-derive them with the aid of Spinors`.
6.2. Existence of a Killing spinor
The existence of a Killing spinor imposes restrictions on the Weyl spinor. To find them, we start by taking the derivative of the Killing spinor condition.
In[194]:=
![]()
Out[194]=
![]()
We decompose each term of this sum into irreducible parts by making use of the "box operator".
In[195]:=
![]()
Out[195]=
![]()
The action of the box operator is computed next.
In[196]:=
![]()
Out[196]=
![]()
We decompose the curvature spinor into irreducible parts.
In[197]:=
![]()
Out[197]=
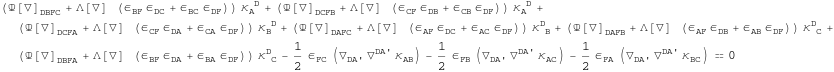
In[198]:=
![]()
Out[198]=
![]()
We are only interested in the symmetric part of this expression.
In[199]:=
![]()
In[200]:=
![]()
Out[200]=
![]()
We will refer to this condition as the Killing spinor integrability condition.
In[201]:=
![]()
This algebraic condition implies that the algebraic type of the Weyl spinor can be only D or N.
6.3. Conformal Killing-Yano tensors
We are going to find the tensor representation of the Killing spinor condition. To that end we define an antisymmetric tensor and its spinor counterpart.
In[202]:=
![]()
![]()
In[203]:=
![]()
![]()
![]()
The spinor ![]() is defined by the condition:
is defined by the condition:
In[204]:=
![]()
Out[204]=
![]()
This entails:
In[205]:=
![]()
Out[205]=
![]()
In[206]:=
![]()
Out[206]=
![]()
In[207]:=
![]()
Out[207]=
![]()
In[208]:=
![]()
Out[208]=
![]()
In[209]:=
![]()
We need to compute the complex conjugate of this rule
In[210]:=
![]()
Out[210]=
![]()
In[211]:=
![]()
Out[211]=
![]()
In[212]:=
![]()
We can now proceed to the computation of the spinor form of the Killing spinor condition. First of all, we need to have as many primed indices as unprimed ones and we achieve this by multiplying by ![]() on both sides of the Killing spinor condition.
on both sides of the Killing spinor condition.
In[213]:=
![]()
Out[213]=
![]()
This can be now transformed into a tensor expression.
In[214]:=
![]()
Out[214]=
![]()
In[215]:=
![]()
Out[215]=
![]()
We replace ![]() by the expression in terms of
by the expression in terms of ![]() found above.
found above.
In[216]:=
![]()
Out[216]=
![]()
We get rid of spinor indices in the covariant derivatives.
In[217]:=
![]()
Out[217]=
![]()
Finally, we replace the product of soldering form by products of "tetra-metrics". This eliminates all the spinor indices.
In[218]:=
![]()
Out[218]=
![]()
All the quantities appearing in previous expression are tensorial, so we may replace the spin covariant derivative by the Levi-Civita covariant derivative.
In[219]:=
![]()
Out[219]=
![]()
In[220]:=
![]()
Out[220]=
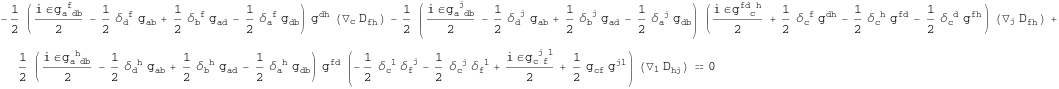
In[221]:=
![]()
Out[221]=
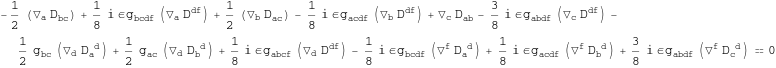
In[222]:=
![]()
Out[222]=
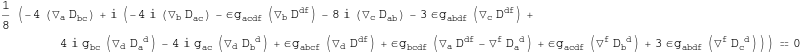
In[223]:=
![]()
Out[223]=
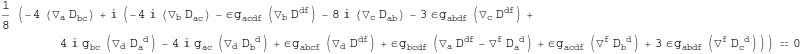
We split this expression into real and imaginary parts.
In[224]:=
![]()
Out[224]=
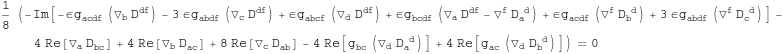
In[225]:=
![]()
Out[225]=
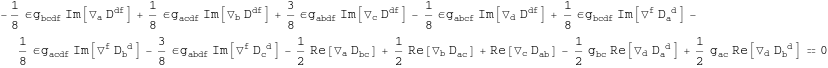
In[226]:=
![]()
Out[226]=
![]()
In[227]:=
![]()
Out[227]=
![]()
In[228]:=
![]()
Out[228]=
![]()
In[229]:=
![]()
Out[229]=
![]()
In[230]:=
![]()
Out[230]=
![]()
In[231]:=
![]()
Out[231]=
![]()
In[232]:=
![]()
In[233]:=
![]()
Out[233]=
![]()
6.3. Conformal Killing tensors
In[234]:=
![]()
![]()
In[235]:=
![]()
![]()
![]()
Consider the following quantity
In[236]:=
![]()
Out[236]=
![]()
In[237]:=
![]()
Out[237]=
![]()
We compute the tensor equivalent of this
In[238]:=
![]()
Out[238]=
![]()
In[239]:=
![]()
Out[239]=
![]()
In[240]:=
![]()
Out[240]=
![]()
In[241]:=
![]()
Out[241]=
![]()
In[242]:=
![]()
Out[242]=
![]()
In[243]:=
![]()
Out[243]=
![]()
In[244]:=
![]()
We check next that ![]() is indeed a conformal Killing tensor.
is indeed a conformal Killing tensor.
In[245]:=
![]()
Out[245]=
![]()
In[246]:=
![]()
Out[246]=
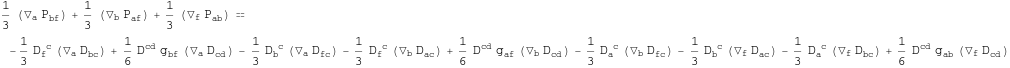
In[247]:=
![]()
Out[247]=
![]()
In[248]:=
![]()
Out[248]=
![]()
In[249]:=
![]()
Out[249]=
![]()
In[250]:=
![]()
Out[250]=
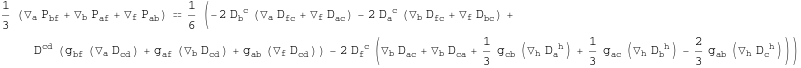
In[251]:=
![]()
Out[251]=
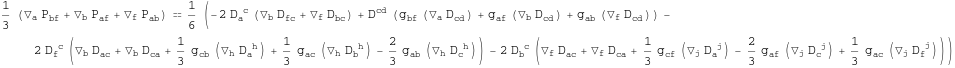
In[252]:=
![]()
Out[252]=
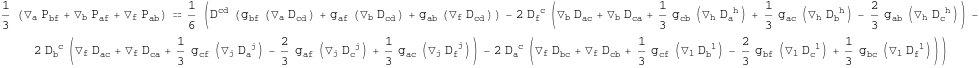
In[253]:=
![]()
Out[253]=
![]()
In[254]:=
![]()
Out[254]=
![]()
In[255]:=
![]()
Out[255]=
![]()
By looking at this expression we realize that ![]() is the trace-free part of a Killing tensor if and only if
is the trace-free part of a Killing tensor if and only if
7. Example: the Dirac equation
7.1. The Dirac Bundle
We define the vector bundle which will contain the Dirac spinors. This is a direct sum of the vector bundles Spin and Spin†.
In[256]:=
![]()
![]()
![]()
Extension of the Levi-Civita covariant derivative to the bundle SpinD.
In[257]:=
![]()
![]()
![]()
![]()
![]()
![]()
Definition of the Clifford algebra elements (gamma matrices)
In[258]:=
![]()
![]()
![]()
The Clifford relation is
In[259]:=
![]()
Out[259]=
![]()
The representation of of the Clifford algebra on SpinD is reducible, Spin and Spin† being invariant subspaces. This entails the relations
In[260]:=
![]()
![]()
In[261]:=
![]()
![]()
In[262]:=
![]()
In[263]:=
![]()
![]()
In[264]:=
![]()
![]()
In[265]:=
![]()
Using previous relations, the Clifford relation can be split in two equations in the following way
In[266]:=
![]()
Out[266]=
![]()
In[267]:=
![]()
Out[267]=
![]()
In[268]:=
![]()
Out[268]=
![]()
In[269]:=
![]()
Out[269]=
![]()
We compare these equations with the following algebraic properties fulfilled by the soldering form
In[270]:=
![]()
Out[270]=
![]()
Therefore, we conclude the rules
In[271]:=
![]()
Out[271]=
![]()
We turn these relations into automatic rules.
In[272]:=
![]()
![]()
In[273]:=
![]()
![]()
7.2. The Dirac equation
We define the Dirac spinor (fermion).
In[274]:=
![]()
![]()
![]()
We define the fermion mass
In[275]:=
![]()
![]()
This is the Dirac equation as it is usually presented in textbooks.
In[276]:=
![]()
Out[276]=
![]()
We wish to write this equation in terms of spinors defined in Spin and Spin†.
In[277]:=
![]()
Out[277]=
![]()
In[278]:=
![]()
Out[278]=
![]()
The covariant derivative CDd acts now on quantities belonging to Spin and Spin†. Therefore it must be replaced by CDe.
In[279]:=
![]()
Out[279]=
![]()
In[280]:=
![]()
Out[280]=
![]()
We cancel the factor ![]() on each side.
on each side.
In[281]:=
![]()
Out[281]=
![]()
In[282]:=
![]()
It is convenient to introduce two new spinors to represent ![]() and
and ![]()
In[283]:=
![]()
![]()
![]()
In[284]:=
![]()
In[285]:=
![]()
![]()
![]()
In[286]:=
![]()
By definition
In[287]:=
![]()
Out[287]=
![]()
We turn these definitions into automatic rules.
In[288]:=
![]()
![]()
In[289]:=
![]()
![]()
Hence
In[290]:=
![]()
Out[290]=
![]()
Compare this with eq. (4.4.66) of Penrose & Rindler Vol. 1.
7.3. Traces of products of gamma matrices
Traces of an odd number of gamma's are zero:
In[291]:=
![]()
Out[291]=
![]()
In[292]:=
![]()
Out[292]=
![]()
But not traces of an even number :
In[293]:=
![]()
Out[293]=
![]()
In[294]:=
![]()
Out[294]=
![]()
In[295]:=
![]()
Out[295]=
![]()
In[296]:=
![]()
Out[296]=
![]()
In[297]:=
![]()
Out[297]=
![]()
Notes
In[298]:=
![]()
Out[298]=
![]()
In[299]:=
![]()
Out[299]=
![]()
Note: For further information about Spinors`, and to be kept informed about new releases, you may contact the authors electronically at algar@mai.liu.se, garcia@iap.fr. This is SpinorsDoc.nb, the docfile of Spinors`, currently in version 0.9.2.
In[300]:=
![]()