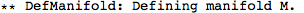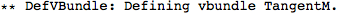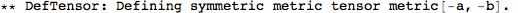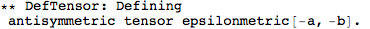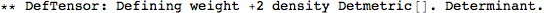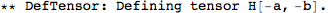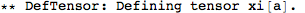Spin 2 on a flat background
This tutorial describes how to construct a gauge invariant theory of a free spin 2 field on a flat background. In doing so, we will recover the linearized Einstein equations.
| MakeContractionAnsatz[expr] | makes an Ansatz with all possible contractions of expr. |
| VarD[tens, cd][expr] | takes the functional derivative of expr w.r.t the tensor tens, while integrating by parts w.r.t. the derivative cd. |
| SolveConstants[expr] | attempts to solve the system expr of tensorial equations for all constant symbols appearing in expr. |
| CollectTensors[expr] | collects all tensorial terms in expr. |
Often used functions for doing field theory.
Setup
First of all, load the
xTras package.
Now we'll set up the manifold ...
... and the metric. Note the option
FlatMetric, to indicate we're in a flat background.
This did not define a new covariant derivative, but instead set the pre-existing partial derivative
PD to be metric compatible with the newly defined
metric. Furthermore, we need to tell the function
SymmetryOf that the metric is constant:
| Out[9]= | 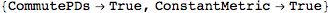 |
Lastly, we need to define tensors for the spin 2 field and its gauge parameter:
The action and the equations of motion
The first step is to construct all possible terms for the action, and make an Ansatz from them. Because we are not interested in total derivative, it suffices to consider terms of the form
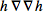
.
| Out[12]= | 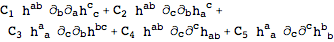 |
The equations of motion are then:
| Out[13]= | 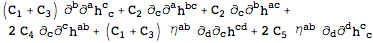 |
Note that there are still some total derivatives present:
| Out[14]= | 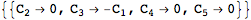 |
If the constant
C3 takes the value
-C1, the action has one total derivative. To eliminate it, we'll set
C1 to zero:
| Out[15]= | 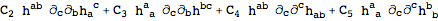 |
| Out[16]= | 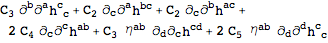 |
Gauge invariance
We impose the following gauge transformation of the spin 2 field:
| Out[17]= | 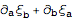 |
The variation of the action is then, up to total derivatives,
| Out[18]= | 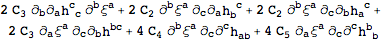 |
We remove any remaining total derivatives integrating by parts w.r.t. the gauge parameter
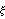
. For this,
VarD comes in handy again:
| Out[19]= | 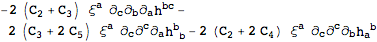 |
For a gauge invariant theory, the above should be zero. Let's solve for the constants:
| Out[20]= | 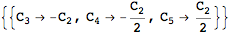 |
This fixed all constant symbols, up to an overall normalization. The gauge invariant action is:
| Out[21]= | 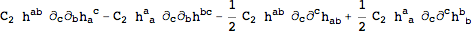 |
And the gauge invariant equations of motion are:
| Out[22]= | 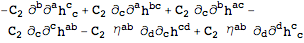 |
These are precisely the linearized Einstein equations.
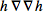 .
.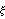 . For this, VarD comes in handy again:
. For this, VarD comes in handy again: