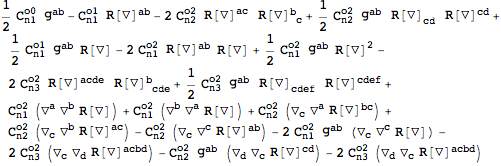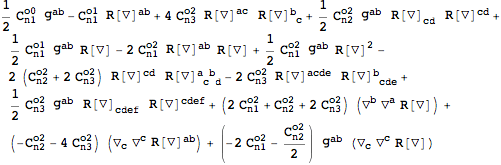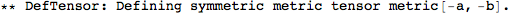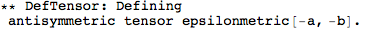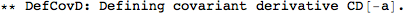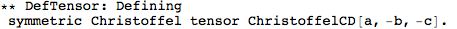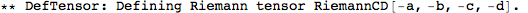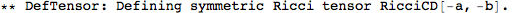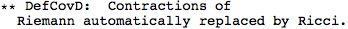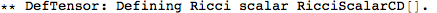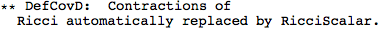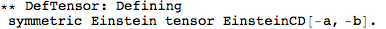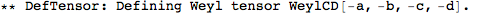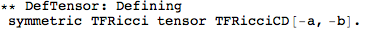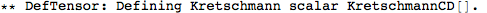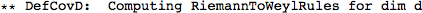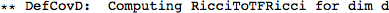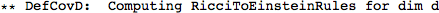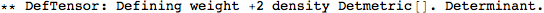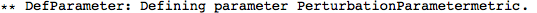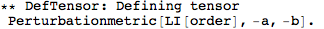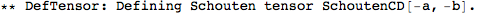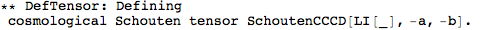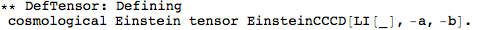Metric Variations
xTras automatically defines 'proper' variations with respect to the metric via
VarD and
VarL whenever you define a metric.
| VarD[g[-a,-b],cd][L] | returns 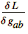 while integrating by parts with respect to the covariant derivative cd. while integrating by parts with respect to the covariant derivative cd. |
| VarL[g[-a,-b],cd][L] | returns 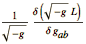 while integrating by parts with respect to the covariant derivative cd. while integrating by parts with respect to the covariant derivative cd. |
Computing variations w.r.t. the metric.
Let's begin with defining a manifold.
DefMetric has a new option,
DefMetricPerturbation. It defaults to True, and so by default a metric perturbation is defined whenever you define a metric.
| Out[10]= | 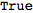 |
In xTras, defining a metric perturbation automatically defines proper metric variations. All in all, defining a metric automatically defines proper metric variations.
We can now perform variations with respect to the metric:
| Out[13]= | 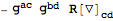 |
Using
VarL automatically takes care of factors of
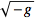
:
| Out[15]= | 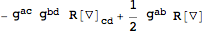 |
Varying with respect to the inverse metric gives an overall minus sign:
| Out[16]= | 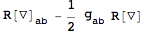 |
| Out[17]= | 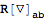 |
More complicated expressions can also be varied easily:
| Out[18]= | 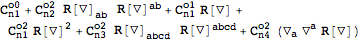 |
| Out[23]= | 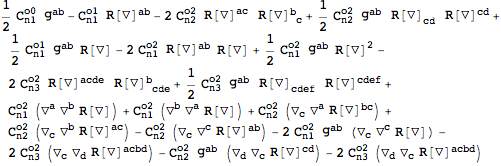 |
This can be simplified further with the help of
FullSimplification:
| Out[24]= | 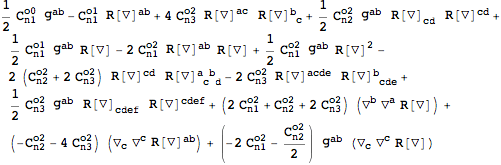 |